Executive Summary
Retirement income guardrails strategies – i.e., planning strategies that predefine thresholds that would trigger an increase or decrease in retirement spending – have been noted to have some significant communication advantages for managing retirement spending expectations. For instance, an approach like Guyton-Klinger’s guardrails – perhaps the most popular guardrails strategy of all – can be presented in a manner that not only tells a client when a spending change would occur, but also how much of a spending increase or decrease would result from ‘hitting’ a guardrail. The caveat to such approaches, however, is that guardrails strategies are generally based on portfolio withdrawal rates, which can be rather crude metrics that may not capture a lot of retiree-specific nuances that could warrant the use of higher or lower guardrails in a given retiree’s situation.
By contrast, one of the most significant strengths of Monte Carlo simulations is their ability to incorporate retiree-specific nuance into a simulation. From capturing unique cash flows and goals to varying longevity assumptions and portfolio composition, Monte Carlo simulations shine in their ability to model scenarios that better reflect a given retiree’s goals and preferences in retirement. The caveat to Monte Carlo simulations, however, is that there are a number of weaknesses regarding the communication and presentation of the results these simulations provide. The common focal point for reporting Monte Carlo simulation results is the ‘probability of success’ of a plan, which is not only often misunderstood by retirees (e.g., by assuming ‘failure’ is more devastating than the ‘adjustment’ that failure scenarios actually imply), but also ignores entire dimensions of planning results (such as the magnitude of spending change) that are crucially important to setting both good short- and long-term retiree expectations regarding retirement income planning.
Fortunately, however, bringing these two approaches together can provide the best of both worlds, as ‘probability-of-success-driven guardrails’ capture both the communication advantages of the guardrails approach and the analytical advantages of Monte Carlo simulation. Essentially, an advisor would define an initial probability of success target (e.g., 95%), an upper probability of success guardrail (e.g., 99%), a lower probability of success guardrail (e.g., 70%), and some spending adjustment rule in the event that a guardrail is hit (e.g., reset to the initial target 95% probability of success). With these parameters in place, an advisor could then solve for dollar values (both portfolio levels and spending levels) that would summarize the guardrails and the changes that would occur in the event that they are hit, and then communicate that to a client, which provides information that is far more insightful to the client than merely telling them what spending level is associated with an X% probability of success.
Furthermore, while software could ideally help speed up the process for advisors and provide some more relevant long-term metrics, the most fundamental advantages of the probability-of-success-driven guardrails approach involve managing shorter-term expectations, which can be captured using even the most basic Monte Carlo simulation software and without ever needing to utter ‘probability of success’ to a client (unless the client wants the detail, of course). Additionally, advisors could easily substitute historical simulation, regime-based Monte Carlo, or other more advanced modeling methods for traditional Monte Carlo simulation at the modeling level, and still carry out the process of communicating results in a simpler and more effective manner to clients.
Ultimately, the key point is simply to acknowledge that probability-of-success-driven guardrails can bring together both the analytical advantages of Monte Carlo simulation and the communication advantages of guardrails approaches, providing advisors with an opportunity to have better conversations with clients regarding their Monte Carlo results!
Guardrails strategies are a popular method for communicating retirement income plans to clients. The Guyton-Klinger guardrails are perhaps the most popular guardrails approach among advisors, but the simple explanation of any guardrails approach is that the “guardrails” serve as the pre-determined thresholds for increasing or decreasing future spending to ‘stay within the guardrails’.
While there’s more nuance to the Guyton-Klinger model, specifically, a very simple example of a guardrails strategy could be to start spending at an initial withdrawal rate of 5% and then to cut spending if withdrawals exceed 6% (which means that spending is outpacing portfolio growth and therefore needs to be reigned in) or to increase spending if withdrawals fall below 4% (where portfolio growth is outpacing spending and builds a cushion to support additional spending).
Here, the lower guardrail is set at 4% and the upper guardrail at 6%; these values serve as the withdrawal-rate-driven guidelines for adjusting spending, and by definition will ensure that the retiree can make it to the end of retirement without fully depleting their portfolio (as at worst, they’ll keep hitting the ‘bad’ guardrail until spending is trimmed enough as a percentage of the portfolio to stay in line). In turn, the guardrail targets – whatever they are – can be specified in a Retirement Policy Statement as a guiding policy for the advisor-retiree to navigate whatever spending changes may be necessary based on whatever the future markets may provide (or not).
The Communication Advantages Of Retirement Spending Guardrails
A retirement spending guardrails approach has a number of advantages when it comes to communicating with clients over the traditional strategy of simply setting a retirement spending target and stating a plan to “monitor the situation and adjust as needed”.
First and foremost, results can be simply conveyed on a one-page financial plan, which helps to avoid overwhelming clients with too much information and keeps the focus on what matters most (whether they’re “within the guardrails” or not and need to make an adjustment to get back on track again).
More generally, a number of key questions that can be succinctly answered within a retirement spending guardrails framework include:
- What is the client’s current distribution rate?
- At what point will the client be able to safely make an upward adjustment in spending?
- At what point would a downward adjustment in spending become necessary?
- If an adjustment can or needs to be made (up or down), how large should that adjustment be?
Presenting all of the above to clients, in actual dollar values, may further help clients to better understand their situation and provide guidance at times when their portfolio might reach key thresholds that could influence their plan… while also highlighting when a change is not necessary (despite any recent market volatility).
For instance, if a client currently has a portfolio of $1 million, and knows an adjustment won’t be needed until their portfolio falls to $800,000, then they may have less concern when they see their portfolio fall to $900,000, knowing that adjustments won’t yet be required at this level. Furthermore, in the event that the decline continues, they already know in advance how much further it can full before they’ll need to cut (another $100,000 decline, or an additional 11% from where the portfolio is now), and how much they’ll need to cut to stay on track even if that decline does occur.
Contrast the wealth of information from a retirement spending guardrails approach with the typical Monte Carlo probability-of-success result. Setting aside all other communication issues with probability-of-success-framed results (e.g., ‘adjustment’ is a more accurate description of a client’s future than ‘failure’, probability-of-success-framing doesn’t convey anything about the magnitude of potential adjustments, such framing could trigger thinking that is prone to the “wrong-side-of-maybe” fallacy, etc.), a probability-of-success result just tells us very little. It does not, for instance, tell us:
- When a retiree would be able to safely increase spending;
- When a retiree would need to decrease spending;
- The size of the adjustment that would be needed to get back on track; or
- Whether the client should even be worried about adjustments, as it is possible that the potential magnitude of failure is so small that it may not even be worth consideration.
In other words, just knowing that the client’s Monte Carlo probability of success has fallen from 95% to 82% doesn’t provide much guidance on whether now is the time to cut spending, how much to cut to get back on track, or what the portfolio would have to rebound to in order to restore spending again (or increase it further from where it originally started).
Moreover, the implications of probability-of-success levels themselves are easily misinterpreted, as the reality is that, so long as plans are updated on an ongoing basis (with corresponding adjustments, as needed), sustainable spending levels are surprisingly similar whether a 50% or a 95% probability of success is used for ongoing planning purposes.
The Analytical Advantages Of Monte Carlo Retirement Projections
Despite the significant communication limitations of probability-of-success-framed results, there are a number of analytical advantages of Monte Carlo simulations over traditional guardrails approaches.
First, in order to be reasonably simplistic for the purposes of implementing and describing to clients, guardrails approaches do have to adopt some rules that could themselves be overly simplistic in a suboptimal way.
For instance, it’s not clear that constant withdrawal-rate-driven guardrail percentages (e.g., always cut if the current withdrawal rate exceeds 6%, and always spend more if the current withdrawal rate falls below 4%) will always make the most sense. It is reasonable to allow withdrawal rates to increase over time, if only to recognize that the remaining retirement time horizon is getting shorter (which generally supports a higher withdrawal rate), and particularly once a client is in very advanced age.
The Guyton-Klinger model does in fact acknowledge this, relaxing guardrail rules for the final 15 years of the projected retirement time horizon, so the point isn’t to criticize any particular model (there can be value in heuristics even when they do oversimplify). Instead, the point is simply to acknowledge that when guardrails are triggered by withdrawal rates, there’s typically going to be some degree of overly simplified rulemaking that will need to be implemented, which then results in potentially missing some client-specific nuances that can be captured via other methods.
Another significant limitation of withdrawal-rate-driven guardrails is that they don’t capture known uneven retiree-specific cashflows and take those into account. As while many clients do spend fairly consistently from year-to-year, if a client does know they have certain sizeable “one-off” spending events (e.g., maybe they want to plan for a $50k new car purchase 5 years from now, 10 years from now, and then 20 years from now), the occasional-but-not-recurring big-spending years are really hard to capture within a guardrails approach. The retiree could try to annualize the expense and back into how much that leaves for other expenses, but that obviates the simplicity of simply dropping the actual planned expense into a plan as can be done with a Monte Carlo simulation.
Furthermore, there are a number of other retiree-specific factors (e.g., life expectancy, portfolio allocation, planned spending changes, QLACs or other future income sources, etc.) that are easy to factor into a Monte Carlo simulation but that, because of the difficulty to capture the retiree-specific nuance, are completely overlooked by most guardrails frameworks.
Getting The Best Of Both Worlds: Probability-Of-Success-Driven Retirement Spending Guardrails
Fortunately, there is a way to capture both the communication advantages of the guardrails framework and the analytical advantages of the Monte Carlo simulation: probability-of-success-driven retirement spending guardrails.
As while withdrawal rates suffer from being hard to maintain at a fixed level that is appropriate over time, the same is not true of probability of success levels. For instance, “90% probability of success” – which will be updated to current/future assumptions every time the Monte Carlo analysis is run – is more reasonable as a stable long-term target than “don’t let withdrawals exceed 6%” (which remains the same 6% regardless of how needs and circumstances may have changed over time). Furthermore, probability of success naturally accounts for all of the underlying client-specific messiness that has to be overlooked with withdrawal-rate-driven guardrails in the first place.
However, that doesn’t mean that clients necessarily need to ever hear an advisor utter “probability of success” when reporting their results. If presented within a guardrails framework (e.g., cut spending if probability of success falls below the 80% lower guardrail, and increase spending if the probability of success exceeds the 99% upper guardrail), but converted and expressed to clients in dollar amounts (e.g., cut spending when wealth drops below $800,000 [80% lower guardrail], and increase spending when wealth rises above $1.2M [99% upper guardrail]), then there’s ultimately very little difference to the client between the probability-of-success-driven guardrails approach and the traditional guardrails approach.
Advisors using Monte Carlo projections for their retirement spending guardrails could still report:
- What the client’s current spending level is (in dollars);
- What portfolio value would trigger a spending decline (in dollars);
- What portfolio value would trigger a spending increase (in dollars); and
- What a subsequent spending increase or decrease would be (in dollars).
Another key advantage of this approach is that it pushes all of the “messiness” (of various assumptions) down to the modeling level. Capital market assumptions, longevity assumptions, and other detailed inputs that Monte Carlo analysis software programs rely on to generate results are captured within the model but are not directly caught up in the results presented to the client, so what the client ends out seeing focuses only on the key results they actually care about.
Furthermore, the client confusion that can come from communicating in terms of “probability of success” is avoided because there’s really no need to talk about probabilities (of success/adjustment) at all!
Instead, the discussion leverages probability of success analyses, yet only focuses on the key pieces of information clients actually want to know (such as the portfolio level when their lifestyle will have to or be able to change). A conversation using the probability-of-success-driven guardrails approach, then, might go something like this (the numbers below are just hypothetical):
Mr. and Mrs. Client, we ran your plan, and here’s what we would recommend. We’d suggest starting at a spending level of $10,000 per month.
If tomorrow your portfolio decreased to roughly $1,800,000, we’d suggest cutting your spending to $9,500 per month.
If tomorrow your portfolio grew to roughly $2,100,000, we’d suggest increasing your spending to $10,500 per month.
It would still be valuable to have access to tools that help clients to understand what frequencies of increases and decreases could be expected over time (as some new tools are capable of) as a means to setting long-term expectations and selecting a retirement income plan that works for a client, but extracting the key insights to communicate to a client without losing the nuance of the modeling is possible with a probability-of-success-driven guardrails approach.
Notably, this approach need not be limited to just Monte Carlo analyses either (e.g., we could target some success/failure percentages based on historical simulations; we could also implement the same approach using “regime-based” Monte Carlo or other similar methods), but for most advisors, the biggest opportunity is simply to go beyond the fairly standard Monte Carlo simulation (and its probability of success results) and to frame within a guardrails context instead.
What A Probability-Of-Success-Driven Retirement Guardrails Strategy Could Look Like In Practice
How Probability-Of-Success-Driven Guardrails Can Set Short-Term Expectations
Let’s look at a simple case study to see how a retirement spending guardrails strategy could actually work out in practice.
Suppose we have the following client couple:
- Dave (66) and Stacy (64) Johnson are married and live in Florida.
- They have $1,000,000 in a 60/40 portfolio.
- They pay 1.2% in weighted-average management fees (including the advisor’s fee and the underlying expense ratios of their investment holdings).
- Dave has $2,000/month in Social Security income that he is already receiving.
- Stacy has $1,500/month in Social Security income that she is already receiving.
- They would like to plan for a spending path that follows David Blanchett’s “retirement spending smile” and assumes declining spending during retirement (more common among retirees in practice than assumptions of constant inflation-adjusted spending).
Furthermore, let’s assume the following:
- They want to leave $200,000 (inflation-adjusted) for their children.
- They are willing to make adjustments to their spending and do so for whatever adjustment is determined to be necessary. However, for practical purposes, they don’t want to be bothered with any spending adjustments that would amount to less than a 5% increase or decrease in their spending.
The first decision is to pick guardrails to be used for the analysis. While we’ve previously noted that probabilities of success that are much lower than what advisors typically are comfortable with could be prudent in retirement, let’s assume these clients are rather risk-averse and want to limit the possibility that their future income will be reduced significantly. Thus, we choose to adopt an initial target probability of success of 95%, a lower guardrail (i.e., spending decrease trigger) of 80%, and an upper guardrail (i.e., spending increase trigger) of 99%.
In other words, our client will start out at a spending level that provides a 95% probability of success. They will increase their spending if their probability of success rises to 99% and cut their spending if their probability of success falls to 80%. In the event that an increase or a reduction is implemented, we want to smooth their adjustments out somewhat, so we’ll only increase or decrease their spending such that they move 10% of the way back to their target probability of success (95%) within a given time period. And as long as their spending stays within the guardrails, they simply continue on their current spending trajectory.
These are the background details, but unless the client wants to dig into these numbers further, they truly can live in the background. If we want to communicate this better to clients and avoid the issues that are associated with misunderstandings around probability of success, then we may present the clients with something along the lines of the following (numbers below are inclusive of Social Security income):
Mr. and Mrs. Johnson, we ran your plan, and here’s what we would recommend. Given your current Social Security income and your portfolio valued at $1,000,000, we’d suggest starting at a spending level of $6,800 per month. [reflecting the spending level required for an initial 95% success probability]
If tomorrow your portfolio fell to around $800,000, we’d suggest cutting your spending to $6,500 per month. [the spending level that would be triggered after hitting the 80% lower guardrail]
If tomorrow your portfolio grew to about $1,100,000, we’d suggest increasing your spending to $7,100 per month. [the spending level that would be triggered after hitting the 99% upper guardrail]

Nerd Note:
The assumptions presented at the beginning of this section noted that declining spending throughout retirement consistent with Blanchett’s retirement spending smile would be assumed. For a guardrails-based spending strategy like the one illustrated in the example above, increases/decreases are entirely driven by probabilities of success at existing spending levels, so this declining spending assumption is really only relevant with respect to comparisons of ‘planned’ and ‘actual’ spending levels – a topic examined in greater depth in the next section of this article.
What is described above would be equivalent to solving for a 95% probability of success, and then suggesting that spending level to a client. But note how much more information is conveyed via the guardrails framework. We ditched the metric (the 95% probability of success) that conveyed pretty much nothing to the client (and possibly even confused the client), and have instead given them a solid short-term roadmap for what to expect in actual-dollar spending amounts and portfolio thresholds.
Furthermore, unlike a withdrawal-rate-driven guardrails approach, the results presented to the retiree still captured their unique cashflows and goals (e.g., spending more in the earlier years of retirement and decreasing their inflation-adjusted spending in later years).
How Probability-Of-Success-Driven Guardrails Can Set Long-Term Expectations
The process above lays out short-term expectations, but to improve the communication process even further, we may want to help the clients understand potential long-term income experiences. This is particularly important if there’s some uncertainty regarding how risk-averse they want to be with their retirement income planning.
To do so, we can simulate our clients Dave and Stacy going through retirement using the chosen 80% to 99% guardrails strategy. We’ll maintain all of the same assumptions previously mentioned, but now we’re also going to simulate Dave and Stacy using this strategy at every point in time going back through 1871.
The historical simulation provides some additional data points that we can use to help Dave and Stacy set expectations for implementing their strategy:
First, we see that, historically, using this 80% to 99% guardrails strategy resulted in Dave and Stacy being able to spend more than planned 76% of the time (and less than planned only 24% of the time).
In this case, “planned” refers to following Blanchett’s retirement spending smile, so we’re benchmarking against some planned decline, but roughly 3-out-of-4 times, we are seeing retirees would have been able to spend more than initially planned for within historical market return sequences. In fact, on average, retirees would have been able to spend about 17% more than planned, and the best-case scenario was 90% above planned spending.
In the scenarios where Dave and Stacy would have had to spend less than planned, the average shortfall was spending a mere 4% below the planned amount, and the worst-case scenario was just 10% below plan.
Notably, actually modeling out the outcomes using this probability-of-success-driven guardrails strategy gives us a lot more context for understanding potential client income experiences than would either just a vanilla Monte Carlo simulation (e.g., “Mr. and Mrs. Johnson, at this suggested spending level, you have a 95% probability of success” which may cause them to panic about the last 5% “failures” even though it actually takes only a modest adjustment to stay on track in the worst-case scenario) or a typical guardrails strategy (in which case clients may understand the “rules”, but still not necessarily grasp what they might actually experience using that strategy and how much upside or downside it may entail).
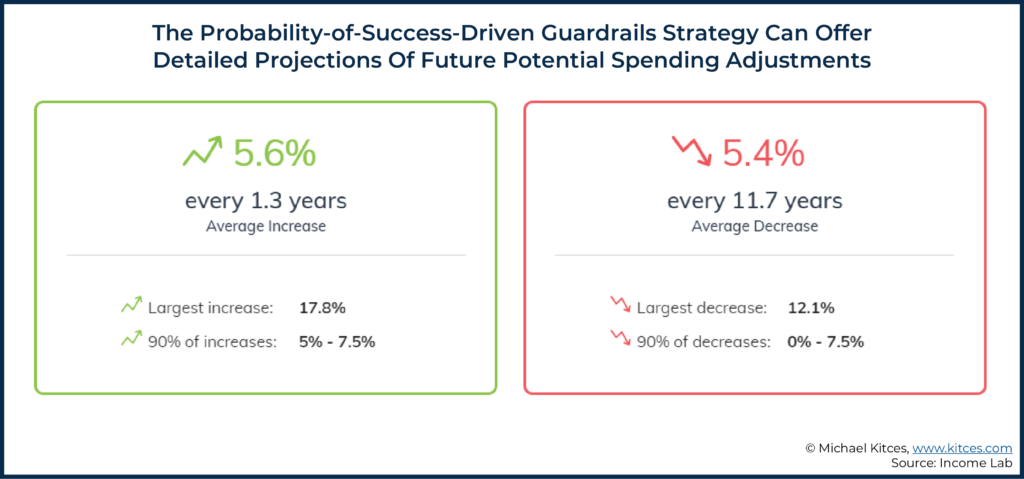
Taking a closer look at income adjustments specifically, we see that, on average, Dave and Stacy experienced a 5.6% increase every 1.3 years and a 5.4% decrease every 11.7 years. The largest increase at any point in time was 17.8%, and the largest decrease at any single point in time was 12.1%.
One important note for Dave and Stacy is to acknowledge that, even using this quite conservative guardrails strategy, there is still some risk of material cumulative cuts. As while the average decrease was “just” 5.4%, there is a possibility that such spending cuts can be triggered more than once in succession.
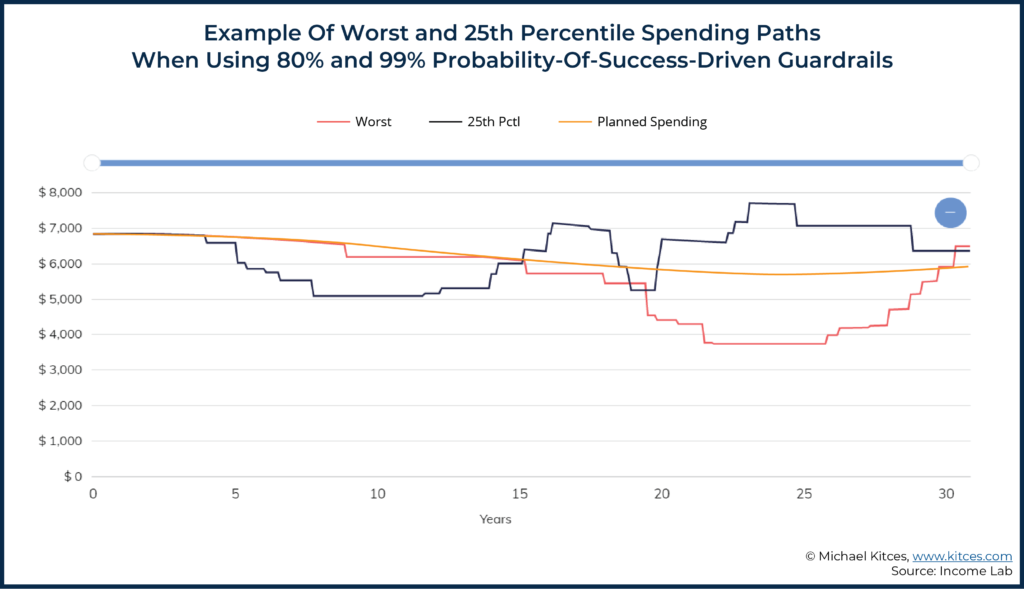
The chart below expresses real spending levels, showing that spending in the worst sequence (red line) bottomed out at $3,756 per month. This represents a 45% reduction off of the initial income of $6,800 per month that was established as the spending level corresponding to a 95% probability of success, but a smaller reduction from planned income since this plan assumed spending would decline according to Blanchett’s spending smile.
Unfortunately, as we’ve previously noted in a similar analysis, minimum and maximum spending levels over a 30-year retirement period are surprisingly similar regardless of the probability of success level used, which means that steep spending declines are possible no matter how conservative a retiree may feel they are with their probability of success threshold chosen. After all, whether the retiree chooses a 90%, 95%, or 99% probability of success baseline, if that 1-in-100 scenario occurs, material spending cuts may still be necessary.
Essentially, when retirees use any kind of dynamic spending strategy and plan to make cuts/increases throughout retirement (as opposed to just trying to spend so conservatively that cuts will never be necessary but the odds are overwhelming that there will be a substantial balance left behind), you more or less get what the market provides, and the probability of success level chosen is more so a trade-off between current income and legacy (i.e., spending more with less likelihood of a legacy, or spending less with reduced risk of cuts but increased likelihood of a sizable legacy amount remaining unspent at the end).
This isn’t unique to probability-of-success-driven guardrails, however, and others have criticized the Guyton-Klinger model specifically for the large cuts that would have been required in some of the worst historical sequences. This is effectively a risk that simply can’t be avoided short of adopting an initial withdrawal rate that is so low that there is virtually no risk of ever running out of money. But for most retirees, eliminating all risk is likely not the optimal solution, as even just a small amount of spending flexibility (that many/most retirees can absorb) is actually associated with significantly higher sustainable spending levels.
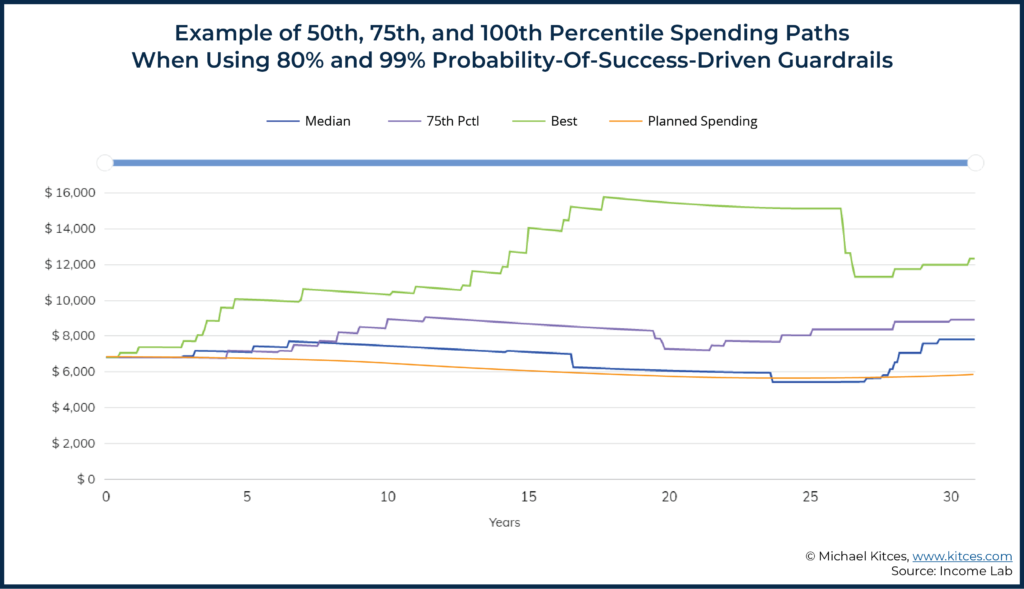
Looking at the more positive outcomes, we see in the graph below that the median scenario was roughly flat in terms of real spending (though note that the “planned” scenario here accounted for decreases in retirement spending consistent with Blanchett’s retirement spending smile, so this spending pattern was actually significantly above the actual “planned” spending initially modeled into the strategy).
Furthermore, the 75th percentile and best outcomes were both significantly higher than initially planned, with real income averaging at close to double the initial spending level for the best-case scenario.
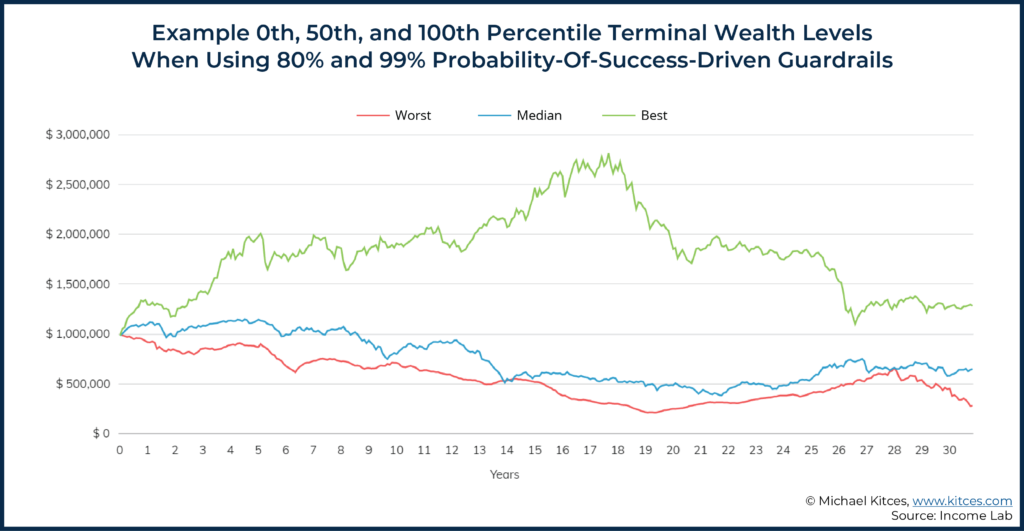
In terms of legacy values, recall that Dave and Stacy had an inflation-adjusted legacy goal of $200,000. As we can see below, even in the worst-case scenario, they still passed on over 41% more than planned (approximately $282,000, as compared to the $200,000 legacy goal originally stated).
Another notable benefit of a probability-of-success-driven guardrails strategy is how much less dispersion we observe in the gap between the minimum and maximum legacy values at any given time compared to typical plan results for standard Monte Carlo simulations.
In the case of Monte Carlo projections, it’s not uncommon to see typical values that range anywhere from $0 to $10,000,000 as being left at the end of the plan, which is a weakness of not modeling out actual changing spending behavior over time.
In simulations with dynamic spending, though, the increased spending rate that would coincide with accumulating very large portfolio values helps avoid the extreme dispersion in estate outcomes and provides a more realistic assessment of where a client’s estate could end up.
The Different Levels Of Implementing Probability-Of-Success-Driven Guardrails With Retirees
There are various ways in which probability-of-success-driven guardrails could be implemented with retirees, ranging from those that are easy to do with existing tools (but that lack much of the communication advantages to those that require time, effort, and software beyond what is offered with typical Monte Carlo simulation programs) to those that may require additional tools to fully capture both the communication and analytical advantages available.
Probability-Of-Success-Driven Guardrails Without Managing Expectations
The simplest implementation of probability-of-success-driven guardrails would be to just run Monte Carlo simulations (without the intent to manage client expectations) and advise a client on when spending changes would be recommended based on guardrails thresholds being reached. In other words, the financial advisor simply updates retirement planning projections on a regular basis, monitors the outcome, and notifies the retiree when a spending change would be advised.
In fact, it is likely that many advisors using Monte Carlo analysis are already using some version of this approach… even if they haven’t articulated it that way (i.e., they recommend a spending cut if the plan’s probability of success gets too low, and may suggest spending more if the probability of success gets too high).
The major disadvantage to this approach is that the advisor doesn’t capture the communication advantages of a guardrails approach. If probability of success is just reported to a retiree with each update (or even reporting nothing but just keeping an eye on it in the background so that the advisor can tell the retiree when to cut/increase spending), then there is a big missed opportunity for managing short-term expectations.
The brilliance of guardrails-type approaches is that the advisor communicates both when a spending change will occur and how much of a change is anticipated to get back on track. That’s tremendously valuable to a retiree in a way that simply telling them they have a “90% probability of success” is not.
Even if the advisor tells the retiree that they have a 90% probability of success and that the advisor will suggest making a change at some lower guardrail threshold (e.g., a 70% probability of success), this still isn’t very useful information from the perspective of managing expectations because the retiree isn’t going to know what it would take for them to get to that 70% probability of success lower guardrail limit, nor would they likely know what change would be recommended at that point to get back on track. The advice given to the retiree here simply remains too abstract.
Fortunately, however, there are solutions for advisors who are willing to put in a bit more time and effort into their plan development process.
Probability-Of-Success-Driven Guardrails With Short-Term Expectations Management
The key to moving past simplistic reporting that means almost nothing to a retiree (e.g., “We ran your plan, and you have an X% probability of success”) is to take the extra step to compute both portfolio values that would hit the guardrails and the spending changes that would be necessary after that guardrail was triggered. Which in effect would give retirees some understanding of when they might expect their plan to require immediate changes and the magnitude of what those changes would be.
Notably, the metrics above are best expressed in dollars and NOT probabilities, percentages, etc. The complexity associated with probabilities and other more abstract statistics can live behind the scenes at the modeling stage and, while important, don’t need to be communicated to the retiree (unless, of course, they want you to explain these aspects of their plan to them!). Because in the end, our brains don’t actually process probabilistic information very effectively.
What the advisor is really going for here are the metrics that actually mean something to retirees… and portfolio values and spending changes are probably the two most important metrics for those relying on their portfolio for spending!
The process to compute portfolio values that hit guardrails is fairly straightforward: Just increase/decrease the retiree’s portfolio values until the guardrail threshold (i.e., target upper or lower Monte Carlo probability of success threshold) is hit. Ideally, planning software programs would automate this process for you (some products are actually available that can do this), but even if the advisor’s software can’t do so automatically, the advisor can still do the process themselves manually (or, better yet, delegate the task to support staff that are capable of carrying out these types of analyses, if available).
For instance, suppose the advisor wants to use a strategy similar to the 80% (lower) to 99% (upper) guardrails strategy described in the example used earlier in this article. Assuming this is the first plan the advisor has run for the client, and that the advisor is using the same 95% starting point described above, then the advisor would have first computed their 95% probability of success spending level, which would be their current recommended spending level.
Example 1: Susan is putting together a financial plan for the first time for her new clients, Dave and Stacy (introduced earlier in the article). Dave and Stacy have a $1,000,000 portfolio and receive $3,500/month in Social Security income.
Susan is starting the plan with a 95% probability-of-success spending level, which would be Dave and Stacy’s current recommended spending level.
If Susan wants to better manage her new clients’ short-term expectations (even using just traditional Monte Carlo software), the first step for her is to compute the spending level that provides a 95% probability of success.
Susan puts this information into her software and finds that $6,800 per month would provide a 95% probability of success for these clients.
Next, the advisor can increase the portfolio values until the plan reaches a 99% probability of success (the portfolio value at this level is reported as the upper guardrail) and then decrease the portfolio values until they reach an 80% probability of success (the balance at this level is reported as the lower guardrail).
Example 2: After Susan determines the spending level that corresponds to a 95% probability of success for Dave and Stacy’s plan, she next seeks to find the portfolio values for each guardrail.
First, she increases the portfolio value until she reaches a 99% probability of success, representing the plan’s upper guardrail. In this case, she finds that the upper guardrail is reached at about $1,100,000.
Then, she uses a similar process to find the lower guardrail, decreasing the portfolio value until she reaches and 80% probability of success, representing the plan’s lower guardrail. In this case, she finds that the lower guardrail is reached at about $800,000.
The next step would be to compute the spending changes that would be needed at a given guardrail to comply with your guardrails strategy. Again following the example above, we were targeting a movement of 10% of the way back to the initial 95% probability of success.
In other words, if the top guardrail (99%) is hit, we’ll adjust spending such that we move 10% of the way back to the initial target (95%), which amounts to increasing spending (at the higher portfolio value) such that the probability of success would fall to 98.6%.
Likewise, if the bottom guardrail is hit (at 80% probability of success), then we would adjust spending such that we move 10% of the way back to the initial target (95%), which amounts to decreasing spending (at the lower portfolio value) such that the probability of success would rise to 81.5%.
Example 3: The next step for Susan is to compute Dave and Stacy’s spending levels at each guardrail portfolio value that would align the probability of success at the guardrail with the target change after hitting the guardrail.
For the upper guardrail (portfolio value of $1,100,000) Susan solves for the spending level that would bring the probability of success at that portfolio value down to 98.6% (i.e., 10% of the way from 99% probability of success down to 95% probability of success, per the adjustment rule being used here). Susan finds that this spending level would be about $7,100 per month.
For the lower guardrail (portfolio value of $800,000), Susan solves for the spending level that would bring probability of success at the portfolio value up to 81.5% (i.e., 10% of the way from 80% probability of success up to 95% probability of success, again per the adjustment rule being used here), which amounts to about $6,500 in this case.
At this point, Susan has now solved for all of the inputs needed to communicate Monte Carlo results to her clients in a way that better manages short-term expectations.
Granted, while the scenario above tries to smooth out spending changes by adopting a more complex adjustment rule (that is easily managed with software but may be harder without), an advisor doing this manually would likely be better off using a simpler adjustment rule, such as adjusting back to a target probability of success more abruptly rather than through a series of smaller changes (so long as clients can tolerate more abrupt spending changes). For illustration consistency, however, we’ll stick with the example above, using 80% and 99% lower and upper guardrails, respectively, and a gradual spending change.
It is important to be careful in thinking about how the advisor frames/reports these thresholds to clients. In particular, since probability-of-success-driven guardrails will always be somewhat of a moving target given the way other underlying assumptions are constantly changing as well (at a minimum, age and life expectancy), the advisor will probably want to speak in rough estimates.
There was some intentionality to the language used in the earlier example that is worth taking a closer look at here (emphasis added for relevance to the current discussion):
Mr. and Mrs. Johnson, we ran your plan, and here’s what we would recommend. Given your current Social Security income and your portfolio valued at $1,000,000, we’d suggest starting at a spending level of $6,800 per month. [reflecting the spending level required for an initial 95% success probability]
If tomorrow your portfolio fell to around $800,000, we’d suggest cutting your spending to $6,500 per month. [the spending level that would be triggered by a 80% lower guardrail]
If tomorrow your portfolio grew to around $1,100,000, we’d suggest increasing your spending to $7,100 per month. [the spending level that would be triggered by a 99% upper guardrail]
The key point here is that, for framing purposes, it probably works well to think in terms of portfolio changes tomorrow and rough (“around $YYY”) portfolio values.
By focusing on portfolio changes tomorrow, the advisor is making it clear that these numbers are assuming that effectively no time has passed. If the advisor does annual meetings with clients and a guardrail is hit 11 months from now, then it is possible, for other reasons, that guardrail has moved around (e.g., the time horizon has also changed slightly, capital market assumptions might have changed, the spending goal may have adjusted, etc.). But the point isn’t to be super precise here, because the more distant future is already imprecise. The advisor is more so just trying to help the client understand when they are in the general ballpark of needing to consider a spending change. (And an actual financial plan update at the time will confirm if it’s the exact threshold to truly take action on a spending change.)
Relatedly, rough portfolio values are helpful because the point here isn’t to pretend to have a false sense of precision. So long as the client knows, “My advisor said we may need to cut spending if our portfolio falls to around $800,000,” then that is enough to set reasonable expectations. If the client does approach the guardrail, then the advisor can re-run the numbers (or better yet, planning software could automatically re-run the numbers for an advisor and alert them accordingly) and see what the best course of action appears to be. More importantly, though, if the portfolio “merely” falls from $1M to $900,000, it’s equally clear to the retiree that such a decline is not one that would merit a spending change (which is actually the more important aspect to soothe a retiree’s nerves in volatile markets).
Overall, the key point here is that the advisor can generate guardrails-style communication even using the simplest of Monte Carlo simulation tools. But it will require some extra steps to solve for the various portfolio values and spending levels that the advisor would report to a client.
Probability-Of-Success-Driven Guardrails With Short-Term & Long-Term Expectations Management
The example above illustrated how existing software tools could be used to capture both the analytical advantages of Monte Carlo simulation and the communication advantages of the guardrails approach for managing short-term client expectations.
Taking this all one step further, however, it may be helpful not only to manage short-term expectations but to help a client establish good long-term expectations. Unfortunately, this is much more difficult – if not impossible – to carry out in the dominant financial planning software programs available on the market today, given that traditional Monte Carlo analysis just tells you what percentage of outcomes were “successful” assuming that a retiree sticks to a pre-defined path, rather than providing insight into how a retiree’s income could change over time using a particular retirement income plan.
More recent entrants to the market—such as Income Lab, Timeline, and Big Picture—are better equipped to provide this type of long-term insight.
Here, the focus should be on helping the retiree understand the long-term implications of different retirement income strategies, so that they can choose a path that best aligns with their own preferences. As a result, conversations around long-term-expectations management are likely most important at the stage of picking a retirement income strategy, although they could continue to be relevant just to help clients stay focused on the long-term.
Therefore, when it comes time to discuss (and choose) a retirement strategy with clients, some relevant metrics to consider reviewing together with those clients include:
- Frequency of typical spending adjustments
- Magnitude of typical spending adjustments
- Magnitude of extreme spending adjustments
- Likelihood of extreme spending adjustments (particularly downward)
- Long-term income/legacy trade-off dynamics
The list above isn’t meant to be exhaustive, but the key point is to focus on metrics that help a client understand what strategies may be right for them (or not!).
As we’ve noted previously, even planning to a constant 95% probability of success would have historically required some quite significant reductions in spending in the last 5% of adverse scenarios to avoid portfolio depletion, so clients that feel like they cannot tolerate the possibility of such large drawdowns may want to target a higher initial probability of success (e.g., 99% or higher), or rely more on income annuities or other guaranteed income streams.
But, in any case, it is hard to have these conversations if you don’t actually have client-specific data that speaks to how such strategies have performed in the past and may be likely to perform in the future.
Ultimately, there are still a lot of nuances surrounding the selection of ideal probability-of-success-driven guardrails that have not been explored (e.g., What is the best probability of success to be targeted initially? How far should a probability of success decline before making an adjustment?), but a probability-of-success-driven guardrails approach can capture both the communication advantages of guardrails frameworks and the analytical advantages of Monte Carlo simulation.
Furthermore, one key advantage of a probability-of-success-driven framework is that it pushes all of the modeling messiness (and industry jargon associated with modeling assumptions) down to the modeling level. Without probability of success itself serving as a focal point, the terminology presented is arguably much less concerning not just for clients, but also particularly for advisors that take the time to understand the nuances of Monte Carlo simulation.
Furthermore, the same probability-of-success-driven framework described here could be thought of as an adjustment-driven framework that allows us to substitute regime-based Monte Carlo, historical analysis, etc. as alternatives for establishing guardrail criteria that would trigger a spending adjustment.
The key point, though, is that a probability-of-success-driven guardrails approach captures the communication advantages of traditional guardrails approaches without overlooking the client-specific cash flow, longevity, and other nuances that are captured in Monte Carlo analyses but that are overlooked by traditional guardrails approaches.
By bringing these two frameworks together, advisors can deliver higher-quality plans for their clients that can also be more effectively communicated to clients.
Disclosure: Derek Tharp is working with Income Lab as a Senior Advisor to help them implement this adjustment-driven retirement spending framework in their software. Income Lab was used in calculating the examples included in this article.






How does an advisor come up with the spending numbers if doing a monte carlo guardrail? Would they need to go into the monte carlo and keep projecting different spending numbers until they hit the goal probablity of success? Guardrails are so easy becomes it instant quick math, would this version require constant fiddling in planning software to find the monte carlo guardrails?
Brian, yes, if an advisor’s software isn’t capable of solving for these values automatically, then the only solution would be to go in and manually calculate the 5 different metrics you would need to report results within a guardrails framework to the client. Those would include:
1. Spending level at the initial/target probability of success
2. Portfolio value that increases the probability of success to the upper guardrail
3. Spending level at the upper guardrail portfolio value that fulfills the upward adjustment rule
4. Portfolio value that decreases the probability of success to the lower guardrail
5. Spending level at the lower guardrail portfolio value that fulfills the downward adjustment rule.
There’s a closed-form expression that quite reasonably approximates the SWR given estimates for expected real return (x̄), volatility (σ), and the number of withdrawal periods (n). The parameter ε sets the “probability of success”, with ε=1 roughly corresponding to a 90th percentile outcome (or 90% probability of success). https://uploads.disquscdn.com/images/5def47713c0c41e75db310166ddca9b8ddf177aeb91c0446a27a58b5eef3be44.png
At first glance, I think that rearranging the equation could give you the values you’d need to present the guardrail parameters without having to use iteration (or perhaps using the closed-form solution as an initial estimate of the parameters to reduce computational intensity).
I’m not a financial planner just an interested retiree…. wasn’t clear to me throughout if you were talking about aggregate spending or just portfolio withdrawals. Does the $6800 per month include the $3500 they get from Social Security or is it a separate withdrawal from their portfolio? Is their starting spending $6800 or $10,300? Quite a difference between the two!
Sorry for the confusion! The numbers reported above were aggregate spending (e.g., $6,800 includes the $3,500 of Social Security income).
This article is a red flag that the Monte Carlo simulator model is irrelevant to retirement planning. Whenever more and more complexity is needed for a seeming simple model then there is something wrong with the model. For example, consider the geo centric model of astronomy which went through such a progression over several centuries.
The Monte Carlo simulator fixes spending and computes the plan surplus or deficit. In order to make its output more relevant bells and whistles such as guardrails have to be added. All manner of papers have been published about how to come up with the initial spending rate. (e.g. 4% rule) The net result is the advisors dance needed to explain the results to the client.
Turn the model inside out and you have an optimization model that fixes the plan surplus and maximizes spending. If you go to bogleheads.org you will see that i-orp.com is just such a retirement calculator that is their go-to resource for evaluating retirement policy issues.
We use Money Guide Elite. I just called them and they said there isn’t an easy way to calculate the guardrails. We can adjust spending levels to see changes in Probability of Success but we can’t alter portfolio values (at least not that I’m aware). Is there a manual way to calculate guardrails within Excel?
Many advisors do use Excel to calculate withdrawal-rate-driven guardrails. Given the restrictions it sounds like you have in place, in order to implement probability-of-success-driven guardrails you may need to create your own Monte Carlo simulator within Excel (which is feasible, but probably not the solution most advisors are looking for) or find some other workaround within your software (I agree with Steve’s comment that you could potentially make this work by adding a large immediate cash flow, either in or out).
Could you adjust the portfolio value by entering a big spend on something at a given moment in time?
I think this would work. Might need to be careful regarding taxes, assumptions for excess cash flows, etc., but a large cash flow (in or out) should be able to achieve at least an approximation of a change in portfolio value. Adding a held away asset might be another way to increase the portfolio value on the upside.
We will be in process of developing an excel calculator for testing. Anyone interested?
we all have needs to know about how much money we can spend… before your even born……. or end up …… or before you end up .waking up on park bench little league field after sleeping off the early am… wholesaler that you may taking you out nxt
this article is a good one to dust off anytime. why not again as the boomers leave the work force in droves. one thing not illuminated for a portion of the assets using an annuity with income rider for guaranteed lifetime monthly income =75% of cash flow needs increases >100% probability. I remember seeing this for the first few times within the FP software I was using. it was an eye opener to myself. to the ah ha moment when an advisor first convinces himself the strategy is bulletproof. takes me back to my prudential days, I didnt know how to feel about some of the finanicial products we were “offering”. Those were my own webs to untangle but luckily I had good mentors.