Executive Summary
One of the key challenges of determining “reasonable” spending in retirement is that, even if the advisor is right about the anticipated long-term returns of the retirement portfolio, there’s a risk that ongoing withdrawals on top of a series of early bad returns will cause the portfolio to be fully depleted before the good returns finally arrive to average out in the long run. As a result, retirees must generally spend less than what expected returns alone would otherwise predict is affordable, to defend against this “sequence of return risk”.
Yet the caveat is that while a bad sequence of returns coupled with ongoing withdrawals can catastrophically deplete a portfolio too quickly, a good sequence of returns can quickly compound the portfolio so far ahead that substantial excess wealth accrues instead. In fact, because of how long-term returns compound to the upside, favorable sequences of returns actually produce far more excess wealth than unfavorable sequences risk to the downside. For instance, taking a 4% initial withdrawal rate has an equal (10%) likelihood of leaving all the retiree’s principal left over at the end of retirement… or leaving 6X the starting account balance remaining instead.
Which means not only is it important to give at least some consideration to the potential and upside “risk” of getting a favorable sequence of returns, but the asymmetric nature of sequence risk to the upside suggests that simply spending conservatively and adjusting later if a “good” surprise occurs may be too likely to leave dramatic levels of unspent wealth that could have been enjoyed earlier. After all, at a 4% initial withdrawal rate, the odds of nearly depleting the portfolio are equal to the odds of growing it by more than 800%(!), and even at a 5% withdrawal rate, the odds of depleting the portfolio early are equal to the odds of tripling the retiree’s starting principal on top of taking an initial withdrawal rate of 5% with 30 years of annual inflation adjustments.
So what’s the alternative? To plan, in advance, for retirement spending strategies to be more dynamic… at minimum, to have a ratcheting plan in place to lift a low initial spending rate higher if the sequence is favorable (or at least, is not unfavorable), and for those who are willing to be more flexible in their retirement spending, to set guardrails in advance to know both when to cut spending in a bad sequence, and when to lift it higher in a more favorable one.
The bottom line, though, is simply to recognize that sequence of return risk truly cuts both ways, creating both the risk of depleting a portfolio too early with a bad sequence (even if returns do average out in the long run), but also the risk of the retiree waiting too long to fully spend and failing to enjoy the assets and income that turned out to be available because a favorable sequence of returns occurred instead!
Sequence Of Return Risk And Withdrawal Rates
Long-term rates of return on a balanced portfolio would suggest that investors should be able to spend at least 6% of their starting account balance in retirement, adjust their spending each year for inflation, and still be able to maintain their spending (adjusting for 3%/year inflation) for 30 years.
After all, the long-term return on an annually rebalancing 60/40 portfolio of simply large-cap US stocks and intermediate government bonds is upwards of 8% since the 1920s, which leaves more than enough room for annual inflation adjustments and still not deplete the portfolio. In fact, even after 30 years of inflation, the bulk of the principal would still be left over if taking a 6% initial withdrawal rate against a portfolio with an 8% long-term return.
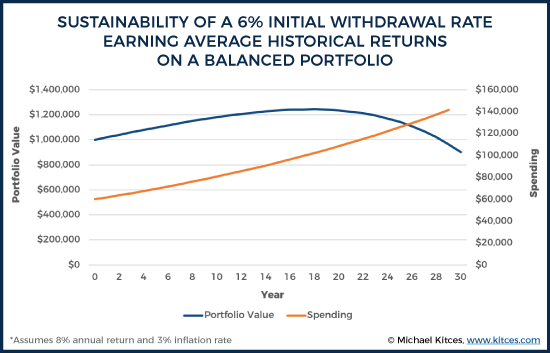
Of course, it may be difficult to get long-term returns comparable to the historical average for those retiring today when bond yields are below-average and stock valuations are high, but even if we look at the worst 30-year returns for a balanced portfolio – a 6.28% compound annual growth rate for an investor starting in 1929 – an investor could still sustain an initial withdrawal rate of almost 5.4% and only barely run out of money at the end of the 30th year.
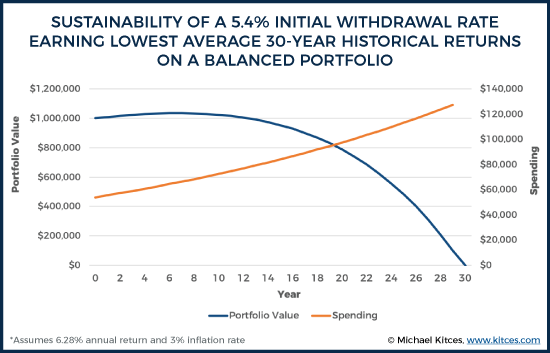
The caveat, however, is the phenomenon known as sequence of return risk, which reveals that even if long-term returns average out in the long run, it doesn’t necessarily mean the portfolio can sustain ongoing withdrawals with volatile returns in the meantime. As a result, even though an initial withdrawal rate of 6% more-than-“works” with long-term average returns, and a 5.4% initial withdrawal rate still “works” with the lowest 30-year growth rate for a balanced portfolio… in practice, those withdrawal rates have a remarkably high risk of failure.
In fact, as the chart below shows, taking even “just” a 5% initial withdrawal rate (and adjusting spending for inflation in each subsequent year) actually runs out of money in nearly 25% of historical scenarios… even though a higher 5.4% withdrawal rate “worked” when projecting the lowest 30-year average returns in history!
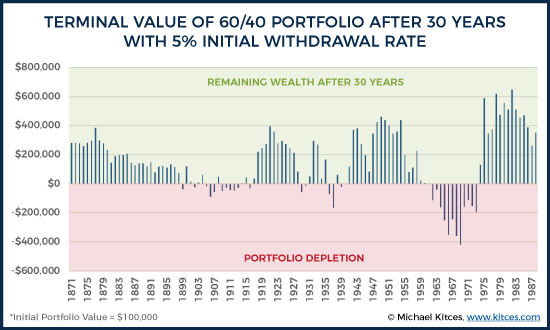
Accordingly, it turns out that to survive all the potential bad sequences that have occurred in history, it’s necessary to take out “just” 4% of the initial account balance (adjusting the spending in subsequent years for inflation) to ensure that the retirement portfolio always makes it to the end!
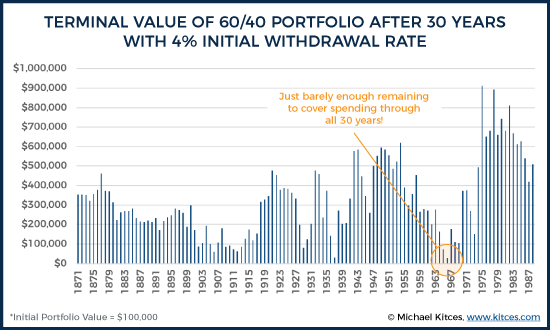
Notably, though, there is actually remarkably little connection between the 30-year return of the 60/40 rebalanced portfolio, and the sustainable initial withdrawal rate itself. As while the safe withdrawal rate of barely over 4% emerges for a 1966 retiree, the 30-year compound annual growth rate for a 1966 retiree was actually 9.56%/year! By contrast, a 1937 retiree also faced a safe initial withdrawal rate of “just” over 4% but had a 30-year return of only 7.24%. And a 1912 retiree had a 30-year compound growth rate of only 5.50% on a 60/40 annually rebalanced portfolio, but was still able to sustain a higher 4.6% withdrawal rate!
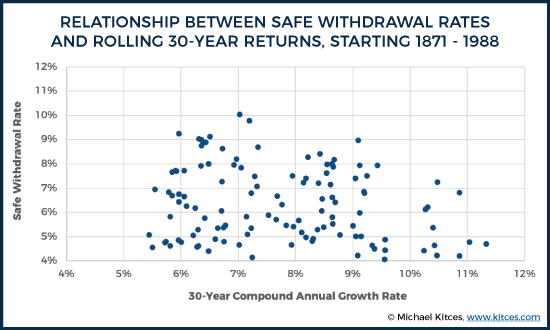
Simply put… the sustainability of portfolio withdrawals is driven far more by the sequence of returns that occur, than the actual long-term return itself. As investors earning long-term returns anywhere between 5.5% and 9.5% necessitated the “same” 4% safe withdrawal rate! Even as an 1874 retiree had only a 5.96% 30-year return but was able to sustain a more-than-double safe withdrawal rate of over 9.2%!
The Upside Potential Of Sequence Of Return Risk
The fact that return sequences can turn out to be so unfavorable, and create an incredibly wide range of potential outcomes for even “similar” long-term returns, is precisely why, even though the average historical return on a balanced portfolio is nearly 8%, it’s not safe to even withdraw at “just” a 6% initial withdrawal rate and be safe. In essence, the fact that an unfavorable sequence of returns could happen means that the retiree must withdraw far less, “just in case.” Thus the evolution of the 4% safe withdrawal rate (low enough to have worked in 100% of available historical scenarios).
Yet the reality remains that by withdrawing at “only” a 4% initial withdrawal rate, the overwhelming majority of the time retirees just finish with a massive excess amount of assets left over!
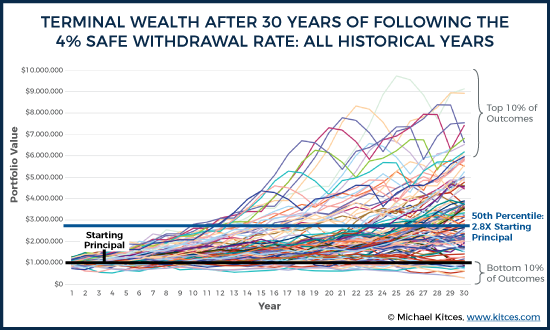
As the chart shows, on average a 4% initial withdrawal rate results in the retiree finishing with nearly triple the original principal, on top of sustaining an initial withdrawal rate of 4% adjusted annually for inflation! In fact, in only 10% of the scenarios does the retiree even finish with less than 100% of their starting principal (and in only one of those scenarios does the final value run all the way down to having nothing at the end, which of course is what defines the 4% initial withdrawal as “safe” in the first place).
By contrast, while the retiree has only a 10% chance of finishing with less than 100% of their starting principal, they have an equally likely chance of finishing with more than 6X their starting principal as well! In other words, the retiree who starts out with $1M in a portfolio at a 4% initial withdrawal rate is equally likely to finish with less than $1M, or more than $6M, after 30 years! And just as the portfolio winds down to $0 in the one worst scenario… it also finishes at more than $9M in the one best historical scenario!

In essence, while sequence of returns risk has the potential for significant downside for a retiree who may have otherwise have a reasonable long-term return but happened to generate them in an unfavorable sequence… it also has substantial upside potential, too!
Dynamic Spending Rules To Account For The Dispersion Of Return Sequences?
While sequence of returns risk can cut both ways – to the downside, and the upside – the irony is that due to the compounding nature of wealth, the reality is that when the sequence is good, it can actually produce exponentially more wealth to the upside than the bad scenarios produce to the downside! Thus why, for a $1M portfolio, there’s an equally likely probability to finish with the same $1M in principal remaining, or $6M left over instead! And even at a 5% initial withdrawal rate, the 25% chance of depleting the portfolio that advisors might caution clients about is the same as the 25% chance of finishing with nearly triple the original principal instead (on top of that 5% initial withdrawal rate with a lifetime of inflation adjustments)!
Of course, the reality from the advisor’s perspective is that the approach of “let’s spend little enough that we make sure we don’t run out of money… and we’ll deal with the upside later,” which effectively puts all the weight on the downside scenario over the upside version, isn’t the worst strategic approach to retirement planning. In practice, it both avoids (or at least reduces) the risk that the advisor is ever sued (e.g., if/when a client spending more gets a bad sequence and really does run out of money), and it simply aligns well to most people’s spending habits, where it’s far more traumatic to cut their lifestyle in a bad sequence than to simply increase it later in a good one.
Nonetheless, the key point remains that dialing down spending to manage sequence of return risk – a la the traditional 4% rule as a means to “avoid running out” of money – almost always produces excess wealth, and in favorable sequences can produce dramatic levels of “excess” wealth. As the odds that a low withdrawal rate preserves principal in bad sequences is equally likely to produce 3X or 6X wealth or more in an equally-likely favorable sequence.
Which raises interesting questions about whether advisors (and retirees in general) perhaps focus too much on the risk of having their retirement portfolio go to $0, and not enough on the “equal” risk of having it rise by 3X or 6X and “underspending” their retirement assets. Or alternatively, whether there’s simply too much focus on setting a low enough withdrawal rate to be “safe” upfront, instead of trying to determine the best approach to dynamically adjust spending along the way.
One way to handle the situation is simply to use a “ratcheting” rule, where spending is ratcheted higher if/when/as a favorable sequence occurs; for instance, the retiree might start with a 4% initial withdrawal rate, but with a plan to increase spending by 10% anytime the current portfolio is up at least 50% from where it started, to be revisited every 3 years. In good sequences, spending will rise over time to consume the otherwise “excess” retirement assets, but in bad sequences, spending is low enough to sustain.
Another dynamic spending approach would be a version of Guyton’s “guardrails,” where the portfolio’s current withdrawal rate is monitored on an ongoing basis, and adjustments are made if certain critical thresholds are breached. For instance, an initial withdrawal rate of 5%, but if the ongoing withdrawals relative to the portfolio rise above 6% then spending is cut (because spending is dangerously outpacing portfolio growth), while if the withdrawal rate falls below 4% (as portfolio growth outpaces spending growth) then the retiree would get a spending increase. The end result is a spending rate that adjusts dynamically as the sequence unfolds… with the potential for cuts if the sequence is unfavorable, but also the potential for raises if the sequence turns out to be more positive.
Unfortunately, modern retirement planning software is very limited in its ability to model such dynamic spending strategies, with only a few recent solutions emerging that can help to illustrate the benefits of planning in advance for making at least some mid-course spending adjustments.
Regardless of the particular dynamic spending approach, though, the challenge is simply to recognize that, because sequence of return risk cuts both ways, conservative spending strategies to manage worst-case sequences can leave absolutely stunning amounts of excess wealth in a favorable (or even merely “not horrible”) sequence. Which means at a minimum, some strategy should be considered. Not that it’s a terrible outcome to simply be “surprised” by the upside of wealth. But given that retirees tend to naturally decrease their spending, without a plan for favorable sequences of returns, there’s a material risk that by the time the retiree realizes they’re on a favorable path, there won’t be enough time and opportunity left to enjoy it.
Or stated more simply: if an initial withdrawal rate of 5% has an equal likelihood of running out of money or tripling in value over the span of retirement… does it still seem too risky? Or is it less about the risk itself, and more about simply having a plan to make adjustments – for the potential of either good sequences or bad sequences – along the way?




How would a more conservative 40/60 allocation effect this analysis?
First of all an 8% return is unrealistic for a retiree with a balanced portfolio of 55% to 60% stock. 5% to 6% is more realistic.There is an easy way to avoid sequence of return risk – don’t withdraw from the asset class that is down in value. Be well diversified and draw from the high quality bond side when the stock side is down. The stock allocation will have decreased with market declines, to rebalance pull from the bond side. Once the stock side recovers – even two to three years – start pulling from the stock side.
Why are flexible withdrawals so rarely mentioned? Withdraw the same percentage of the portfolio each year. The portfolio goes up, you withdraw more, it goes down, you withdraw less. Why this obsession with a fixed withdrawal rate?
Because retiree’s don’t really want their spending to be so variable year over year. They want to set a standard and living and try to maintain that throughout retirement.
FWIW, my wife and I are in our 6th year of retirement. So this is something we deal with every year (it is not theoretical).
The pillar on which this stands – ‘average returns’ also needs to be more dynamically monitored