Executive Summary
One of the most common criticisms to the use of Monte Carlo in financial planning is its typical assumption that investment returns are normally distributed, when in reality the market appears to go through environments that may be more volatile than a normal distribution would predict, as highlighted by the events of the financial crisis. In the last four months of 2008 alone, the market experienced 20 high-volatility trading days with a standard deviation varying from 3.5 to almost 10... each of which should not have occurred more frequently than once per millenia to once per several billion years. Yet when we look at those returns on an annual basis, we see a very different picture - the one-year decline to the bottom in March of 2009 was a "mere" 2.5 standard deviation event, which is uncommon but entirely probable under a normal distribution. Which raises the question - are "black swans" just a short-term phenomenon that average out by the end of the year, and are we focusing too much on impossibly rare black swans instead of the rare-but-entirely-probable 2 standard deviation decline?
The inspiration of today's blog post is a continuation of the analysis of black swans I have been working on as a part of my recent series on Monte Carlo analysis in the January and pending February issues of The Kitces Report. In exploring the ongoing criticism of the so-called "black swans" that violate the normal distribution assumption in Monte Carlo planning, I discovered a very interesting fact: black swans seem to be entirely a short term phenomenon.
For instance, the graph below shows the actual daily price volatility (red line) of the Dow Jones Industrial Average for roughly the past century (from 1900 through late 2009) against the frequency of those results that would be expected from a normal distribution (green line). As the results reveal, when looking at the actual historical data, there is a surprising frequency of very extreme results, at least relative to the "0" probability they were anticipated to have. To either side of the green bell curve, we see several small red peaks showing historical data points that could only be termed "extreme outliers" - in fact, the graph has to be widened so far to fit them, that the green line is condensed in the middle and looks more like a green bump than a green bell! (If we zoomed in to only look at the center of the graph, though, the familiar bell-shaped curve would be present.) Although many of the outliers shown by the red line literally represent no more than 1-10 occurrences out of over 27,000 daily data points, the fact that they exist at all is shocking; any result beyond 5 standard deviations should only occur once every several millennia, yet we see numerous instances in this barely-more-than-a-century data set; the most extreme results, at +/- 10 standard deviations (with two data points at almost -20 standard deviations), would not be expected to occur even once in several lifetimes of the universe!
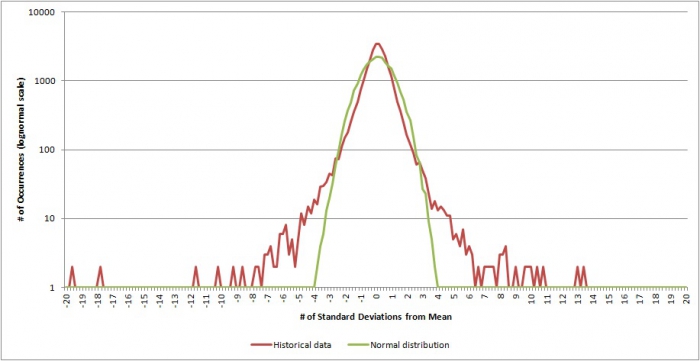
However, it is notable that these results are based on daily return volatility, while in practice financial planning clients are investing for months, years, or even decades at a time, and have relatively modest ongoing withdrawals (or may even still be contributing). It's not as though financial planning clients are invested with extensive leverage, where an extreme short-term event can render them insolvent before a recovery comes. After all, a client who is withdrawing less than 5% of the portfolio in any particular year might not be harmed at all by extreme daily volatility as long as it recovers by the end of the year, and in fact might not be harmed much by a severe one-year portfolio decline, as long as it is followed by an equally volatile recovery in the opposite direction in the subsequent year. And as the above graph highlights, the unexpected "black swans" do occur in the positive direction as well as the negative, creating the genuine potential that positive black swans could largely offset negative ones.
To look at this effect over time, the next graph below shows the distribution of historical market returns when viewed on an annual basis, instead of a daily basis. As the results reveal, in reality over the span of a year, daily negative black swans are in fact offset by positive black swans as mean reversion (and/or the impact of market valuation) takes hold, and consequently the market declines in the historical data on an annual basis are actually remarkably close to what is predicted by a normal distribution! Just as the normal distribution would predict no extreme outliers beyond approximately 3.5 standard deviations in "only" a century of data, the actual results confirm there weren't any!
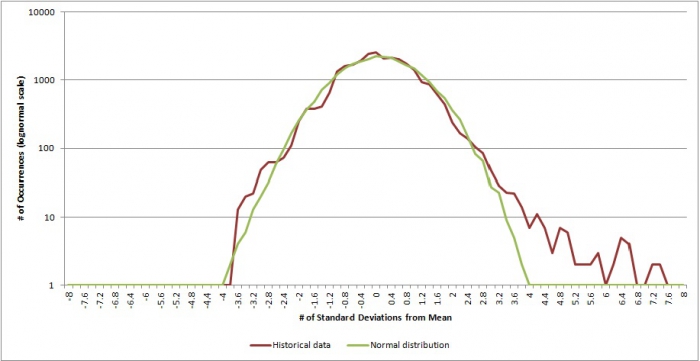
To be fair, if you look closely, it is true that there's a slightly higher frequency of negative results that range from -2.5 to -3.5 standard deviations in the annual data - they should be more rare. Yet on the other hand, there are also an unexpected frequency of positive results in the +2.5 to +3.5 standard deviation range, as well as additional results that extend up past 7 standard deviations! If we were to view all of these unexpected results as "black swans", then the reality is that there are almost as many positive black swans as there are negative ones, when viewed on an annual basis! In other words, the greatest surprise implied by the distribution of actual historical annual returns is an elevated "risk" that the client might turn out to get impossibly rare good returns that would not be predicted in a normal-distribution-based Monte Carlo! Of course, since the returns are positive, they perhaps would be better labeled as "gold" swans than black ones! (Note: Technically, as a series of normal distribution returns compound, they are expected to produce a distribution with an increasingly long positive tail, due to the impact of positive compounding to the right while negative returns are ultimately constrained by the zero bound {you can't have negative wealth}. This distribution is called a lognormal distribution, and in fact some Monte Carlo software is built using a lognormal distribution instead of a normal one. Nonetheless, relative to modeling market returns in Monte Carlo using a normal distribution for annual returns, which is still the most common approach, the fact remains that the normal distribution is more likely to underestimate extremely good returns than extremely bad ones, when viewed on an annual basis.)
Of course, this is not to say that the negative returns on the left side of the annual results can't lead to a disaster in the client's financial plan. A negative 2 standard deviation event is still a pretty bad one-year price decline of roughly 35%. But the point is that a 35% bear market decline in a year is not a black swan - it's a rare but entirely probable event already anticipated by a normal distribution. The only black swans - the events that are predicted to never happen with a normal distribution, yet do - are actually the gold swans.
Which means the real challenge in financial planning, where there is no leverage and spending even over the span of a year is fairly modest relative to the total portfolio, is not dealing with the impact of negative "black swans" but in being prepared for the rare but entirely probable 2-standard-deviation bear market that is likely to occur at some point even under a normal distribution. Which in turn suggests, as highlighted in last week's blog, that managing effective retirement advice is less about dealing with the risk of impossibly rare black swan declines, but more about how you plan and prepare for any kind of decline, including the rare but probable ones.
So what do you think? Are we overreacting to "black swans" in the financial planning context, where there is no leverage and clients have only modest withdrawals at best? Have we become too focused on the extreme black swans, and ignored the rare but entirely probable "normal" bear market decline already predicted by normal distributions? Would you change your planning discussion with clients if the reality was that the only true black swans that occur annually are actually golden?




