Dynamic Programming As A Methodology For Financial Planning Retirement Projections

The Two Tracks Of Retirement Planning Research

Retirement planning research has historically developed along two distinct tracks, which in turn has shaped the kinds of retirement planning strategies and tools that we use today.

Practitioner-Oriented Research On Financial Planning Strategies

Financial planners will likely be most familiar with practitioner-oriented research, particularly given the widely-read Journal of Financial Planning, which is focused on this type of research.

Perhaps the most famous example of this type of practitioner-oriented research is William Bengen’s 4% withdrawal rate study (published in the Journal of Financial Planning in 1994), but practitioner-oriented research would also include the wide range of studies from scholars since Bengen who have examined questions related to how people ought to best plan and save for retirement. Notably, practitioner-oriented research doesn’t actually have to be created by a practitioner (as was the case with Bengen); a key aspect of such research is that generally it is aimed at providing advice regarding how people ought to behave in order to succeed financially. This is what researchers would call a “normative” approach to research, and it is different than a “descriptive” (or “positive”) approach to research, which simply aims to describe reality.

It’s easy to understand why practitioners are drawn to normative research, as the job of a planner is to help clients make decisions. In this context, how people do behave matters much less than how people ought to behave. While the former might help give planners foresight of problems their clients may encounter, it’s the latter that planners spend their time advising clients on. In other words, given that the purpose of financial planning is to help people make good financial decisions, it makes sense that practitioners gravitate towards research which can help facilitate that purpose.

Another notable feature of practitioner-oriented research is that it tends to be practical. Bengen’s 4% rule is useful because it provides answers that can be directly applied to client questions. Practitioner-oriented research tends to lead to either rules of thumb of what people should try to do or achieve, and/or straightforward frameworks for making decisions based on individual goals, circumstances, and trade-offs. As a result, it also tends to be more of a “satisficing” than “optimizing” approach to making decisions.

For instance, whether based on straight-line projections or Monte Carlo analysis, most planners simply help clients evaluate different alternatives until they reach a solution that satisfies their needs. Planners typically don’t run thousands of different scenarios adjusting a large number of variables until they find the one single scenario that provides the “best” outcome available, as might be done under a truly “optimizing” approach (though, it’s reasonable to question how effectively optimization can generally be done in the first place, and to what extent greater precision would actually change the outcome).

Economic Research On Financial Planning Strategies

The second broad branch of financial planning and retirement research comes from economists, who view it as a study of consumption across the life cycle. In contrast to practitioner-oriented research, which primarily focuses on how people ought to behave, economists have historically focused both on how people ought to behave and how they actually do behave.

Some notable developments in the history of economic thought related to retirement planning in particular include Keynes’ (1936) marginal propensity to consume, Duesenberry’s relative income hypothesis (1949), Modigiliani & Brumberg’s (early 1950s) life cycle hypothesis, Freidman’s (1957) permanent income hypothesis, and Shefrin & Thaler’s (1988) behavioral life-cycle hypothesis.

One key component of these theories, at least since Modigiliani & Brumberg, is the idea that people seek to engage in consumption smoothing—i.e., borrowing, saving, and “dissaving” (i.e., spending) across the life cycle in an effort to stabilize their level of consumption throughout their lifetimes.

This approach relies on the economic concept of utility (i.e., satisfaction received from consumption) and individuals are said to have some type of “utility function” which defines their consumption preferences. Models can vary significantly in their complexity and design, but armed with a mathematical representation of how individuals are assumed to rank consumption preferences (quantifying the benefit of spending more versus less, now versus later, etc.), economists can then seek to find conditions which maximize utility and derive conclusions about how consumption behaviors should change as a result.

Dynamic Programming: Where Two Paths Meet?

While both economic and practitioner-oriented retirement research have developed mostly independent of one another, one promising characteristic of dynamic programming is that it provides an avenue to begin to potentially merge these distinct fields of study. Dynamic programming is practical enough that it can be used by practitioners to help clients solve real-world problems, but it is also robust enough to incorporate insights and methods more commonly used by economists – particularly the optimization of consumption and asset allocation decisions across the life cycle.

What Is Dynamic Programming?

To understand what dynamic programming is, it may be helpful to first explore what dynamic programming is not.

Consider straight line projections and Monte Carlo analysis, which are two of the retirement planning methodologies most familiar to financial planners currently. Under straight line projections, every input in a plan is assigned a specific value. For instance, a retiree may be assumed to live 30 years in retirement, hold a 60/40 portfolio, earn 6% per year, spend $50,000 per year, and increase their spending annually with inflation at a rate of 3%. Of course, straight-line projections can be more complex, but the key is that there is no variability within the assumptions. Planners may choose to look at several different scenarios—perhaps comparing the results of a less risky portfolio earning a lower return or prolonging retirement for 35 years instead of 30—but in order to do so, a new straight line projection must be run.

Monte Carlo analyses are mostly the same but introduce the potential for variability. Most commonly, this variability will exist among investment returns. For instance, instead of a 60/40 portfolio earning a constant 6% per year, returns may be assumed to have a mean of 6% and a standard deviation of 10%. Allowing variation in investment returns provides a more realistic range of investment outcomes that a retiree may experience, but the rest of the assumptions are still static. A planner or retiree may again adjust the plan to analyze additional scenarios, but the usual process is more one of satisficing rather than optimizing—i.e., adjustments are made until the retiree is satisfied with the results, rather than truly optimizing across a range of variables.

Understanding Dynamic Programming

Dynamic programming (also known as dynamic optimization) has many applications and is really just a method of solving larger problems by breaking them down into smaller problems. In a 2014 article in The Journal of Retirement, Gordon Irlam and Joesph Tomlinson provide an overview of how dynamic programming can be applied to retirement income research.

From a financial planning perspective, dynamic programming introduces variability to a greater number of planning assumptions, while still allowing (mathematically) for quickly finding optimal solutions based on that given set of assumptions.

For instance, dynamic programming could allow spending (consumption), asset allocation, investment returns, and longevity all to vary at the same time. Adjustments to each could be tested in various combinations, effectively providing a “map” of optimal paths of spending and asset allocation, given the actual investment performance and longevity a retiree experiences, rather than simply testing a particular spending and asset allocation strategy against certain investment and longevity assumptions to “see if the plan works” (and manually change the assumptions if it doesn’t).

Consumption Risk Aversion (Vs Portfolio Risk Tolerance)

Risk aversion is an important concept for understanding the role utility functions play within dynamic programming analysis. While personal and consumer finance researchers often consider financial risk tolerance (i.e., the willingness to tolerate uncertainty) as the theoretical opposite of financial risk aversion (i.e., the unwillingness to tolerate uncertainty) (Grable, 2008), Irlam & Tomlinson’s (2014) overview of dynamic programming views these concepts differently. Specifically, risk aversion refers to the willingness to tolerate fluctuations in consumption whereas risk tolerance refers to the willingness to tolerate downside portfolio loss potential.

For instance, suppose an individual has won a unique lottery where they have a 50/50 chance of receiving either $10,000 or $20,000 annually for the rest of their life. We can assess their consumption risk aversion based on what amount of guaranteed income the individual would accept in lieu of this uncertain proposition.

From a purely expected value perspective, this proposition is worth $15,000 per year (as 50% of the time you get $10,000 and 50% you get $20,000), and an individual who would accept $15,000 in lieu of the risky alternative would be said to be risk neutral. However, most people are assumed to be risk averse, which means we will pay a premium for certainty (i.e., most people will accept some guaranteed number less than $15,000). An individual who is risk averse might accept just $13,000/year if it was guaranteed, rather than having the possibility of receiving $20,000/year but facing the risk of getting only $10,000; by contrast, a less-risk-averse person might still prefer the gamble unless the guaranteed income was at least $14,000/year.

Notably, this is not the same trade-off as portfolio risk tolerance. An individual may have both a high ability to tolerate portfolio risk (high portfolio risk tolerance) and a strong preference for consumption certainty (high consumption risk aversion). Or, viewed another way, just because an investor can maintain their composure and mental state in the face of a high risk of portfolio loss, doesn’t mean that person actually enjoys or prefers consumption uncertainty (and thus, might still choose a guaranteed consumption amount even though they’re willing to tolerate portfolio uncertainty).

While searching for optimal solutions, dynamic programming is primarily concerned with consumption risk aversion, though restrictions could be added to a model to account for portfolio risk tolerance as well (e.g., even if a 100% equity allocation would optimize an individual’s consumption utility function, possible solutions could be bounded to only include those up to 70% in equities).

A Simple Dynamic Programming Example

(Note: The following example is overly simplified and based on Irlam & Tomlinson’s methodology laid out in Retirement Income Research: What Can We Learn From Economics? Irlam’s AACalc software is available for free online and can handle more complex and realistic scenarios.)

As a simplified example to illustrate dynamic programming, suppose John is 70 and knows he will live exactly 5 more years. He’ll be in great health this entire time, but he will not live longer. John receives $15,000 in Social Security income and has a $250,000 Roth IRA with no other assets or liabilities. John is trying to decide how his portfolio should be invested over time.

Further, suppose that John has a moderate level of consumption risk aversion. As a result, dynamic programming might generate an asset allocation map that looks like this:

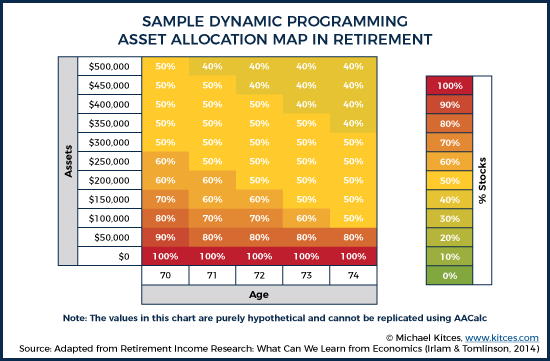
These results show that John’s optimal asset allocation may actually change over time, depending on how his portfolio is performing along the way. The higher his portfolio grows, the smaller the percentage of stocks that he would need to support his retirement goal. Conversely, the lower his portfolio declines—making his total consumption more dependent on Social Security—the more attractive it becomes to place all of his portfolio in stocks with the hopes of catching a bull market. The key point: with dynamic programming it’s not simply a matter of projecting a range of returns around an initial portfolio allocation and selecting the allocation which works "best". Instead, dynamic programming assumes that the portfolio can and would be altered each year — adapting to what has actually happened in the plan up to that point.

Technically, though, the way this map is determined by a dynamic programming analysis is actually to start in the last year of John’s life and then work backward. Given John’s utility function, the program evaluates all possible combinations of consumption and asset allocation at a particular asset level, and then determines the optimal allocation which is indicated in each coordinate of the chart (e.g., 40% equity with a $500,000 portfolio at age 74). After optimizing across all asset levels at age 74, the program continues to solve backward by optimizing values at age 73.

At this point, you can probably see why dynamic programming requires so much computing power – particularly when evaluating longer time horizons and accounting for more granular differences in asset levels, consumption, and asset allocation. With multiple variables over multiple years (or decades), the number of different combinations to test grows exponentially. In practice, different mathematical algorithms can be used to generate results quicker than literally running every single combination of scenarios, but there is still a lot of computation required to generate results.

Further, the asset allocation map generated above is only part of the results generated by a dynamic programming analysis. In addition to optimal asset allocations, dynamic programming generates optimal consumption paths as well. Assuming that an individual has no bequest motives (i.e., they derive no utility from leaving assets to heirs), a greater proportion of remaining wealth would typically be consumed each year until ultimately consuming 100% of remaining wealth in the final year of life (at least if you assume this final year is known).

Of course, rarely do we have reasonable estimates of how much longer we will live (and if we do, it’s usually over a short time horizon), but the use of stochastic (i.e., random) dynamic programming methods do provide the possibility of varying time horizons as well. In other words, one assumption might be to simply assume that in any particular year, the plan is to spend over the individual’s remaining life expectancy, recognizing that the life expectancy time horizon itself will change with each additional year of survival. Furthermore, rather than simply smoothing consumption to be level across time, more realistic modifications—such as the assumption of “impatience” (i.e., that future utility is discounted more than present utility… possibly resulting in declining spending throughout retirement) or the addition of known cash flows to particular years (e.g., planned trips or other goals)—can be utilized to more accurately model utility maximizing consumption paths throughout retirement.

Returning to our example of John’s retirement, we can consider some hypothetical consumption paths based on his particular utility function (i.e., how John would get the most satisfaction from varying levels of consumption in retirement).

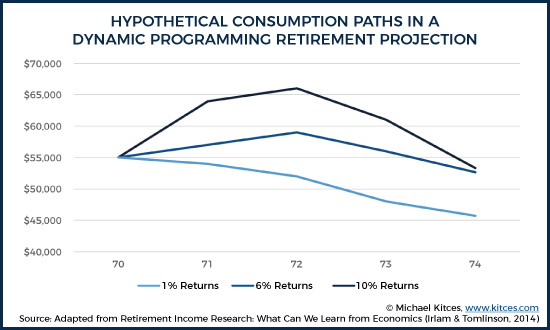
Under each scenario, John starts out consuming $70,000, which includes $15,000 of Social Security income adjusted annually for 3% inflation. Recall that John has a $250,000 Roth IRA, which, based on the asset allocation map shown earlier, suggests he should utilize a 60% equity portfolio at age 70. (Note: To simplify this illustration even further, only portfolio consumption [starting at $55,000 per year] is considered in the charts above and below.)

It’s important to note that there’s more going on here than can be captured in either the asset allocation map or by the consumption spending paths independently. Because dynamic programming can adjust both consumption and asset allocation based on the conditions actually experienced, you can envision each point on the map as having both an asset allocation and a consumption amount associated with it. It is generally easier to think of these in isolation from one another, but the reality is that they are intertwined, in what would look more like a 3-dimensional roadmap.

For purposes of simplification, assume all straight-line returns, with a low returns scenario providing 1% annual returns over this five-year period, an average returns scenario providing a 6% annual return, and a high returns scenario providing 10% annual returns. If this were the case, then John would experience the following:

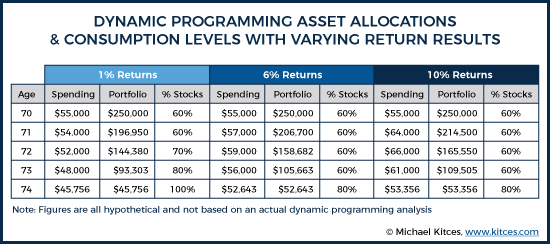
Under the 6% return scenario, at age 71, John would have a Roth IRA worth just shy of $207,000. Based on the asset allocation map (shown earlier), this suggests John would maintain a 60% equity portfolio. By age 72, John’s Roth IRA would have roughly $159,000, indicating he would still maintain a 60% equity portfolio. But consider what would have happened if John actually experienced the low returns scenario (1% annual returns). Under this scenario, not only would have John decreased his consumption by roughly $1,000 at age 71, but at age 72, his portfolio would also only be worth roughly $144,000. Based on the asset allocation map (see example referenced earlier), this would suggest that John actually increases his equity allocation to 70%. While these numbers are purely hypothetical and for illustration purposes only, the point is that the dynamic programming approach is providing a roadmap to how both spending and asset allocation might change, based on what future returns turn out to be. In this hypothetical scenario, given John’s utility function, his guaranteed Social Security income is giving him room to make his portfolio more aggressive in the bad return scenario with the hopes that it rebounds (and knowing that if it doesn’t, Social Security is still making up the majority of his income anyways). Other retirees might have different utility functions that would weigh these trade-offs differently, but the key point is that dynamic programming is providing different courses of action based on the conditions ultimately experienced.

We could then continue this process all the way through John’s life, utilizing his experienced investment returns and consumption to identify the potential paths for his ideal consumption and asset allocation in any subsequent year. This “mapping” process that can be provided by dynamic programming is one of the core benefits of the approach.

Notably, even with a dynamic programming analysis that is designed to account for adjustments over time, some updates may still be appealing. In some cases, that may be because the original projection used simplifying assumptions (e.g., used a fixed retirement time horizon rather than dynamically projecting mortality), such that the plan must be periodically updated for new assumptions. Or, alternatively, the key inputs could vary over time, beyond the scope of what was dynamically programmed. For example, a retiree may receive a cancer diagnosis that materially shifts their mortality curve more than just the assumed changes for getting older. Or it may be the case that the retiree exhibits "time-varying risk aversion" (i.e., their portfolio risk tolerance changes materially over time) as has been investigated by Blanchett, Finke, and Guillemette (2016). As a result, Irlam & Tomlinson (2014) do note the importance of ideally updating dynamic programming projections just as would be done with a traditional financial plan.

Nonetheless, the key point remains that traditional Monte Carlo analysis happens at a single point in time and typically assumes the retiree charges forward blindly with their original spending and asset allocation, regardless of the scenario experienced, while dynamic programming not only assumes adjustments will be made along the way, but it tells us (based on optimization) what those adjustments would need to be as well!

Why Dynamic Programming Matters

As we’ve seen above, one of the main benefits of dynamic programming is that it is truly an optimizing approach rather than a mere satisficing approach as most planning is today. A single dynamic programming analysis also has the potential to provide guidance about what to do now and in the future in a way that a one-time Monte Carlo plan cannot. Assuming no material changes in a retiree’s life expectancy or utility curve, the retiree could identify the path they’ve encountered and make the appropriate adjustments to their consumption and asset allocation, all from the original plan projection.

Dynamic programming also leads to some advice that is significantly different than traditional rules of thumb and ongoing advisor guidance. For instance, while strategies like taking an inflation-adjusted 4% distribution do serve as a means to smoothing consumption (something generally assumed to be desirable under economic models), it’s possible they smooth consumption too much. This is particularly true in light of two important observations: (1) consumption may be more valuable earlier in retirement rather than later, and (2) many retirees just want to spend their money (not too quickly, but enough that they don’t leave over a giant bequest that has no value/utility to them).

The first observation—that consumption utility is not equal across all points in time—implicitly acknowledges considerations such as the fact that while people are young and healthy (i.e., in their “go-go” years of retirement) consumption may be able to buy more satisfaction than it does when they are aging and frail in the “no-go” years of retirement.

There are other rational reasons for retiree “impatience” as well, particularly given the fact that our lives can always come to an end sooner than we wish. Even if we assume an individual maintains consistent health throughout retirement and an adequate asset base to hedge against the opposite concern (i.e., that we live longer than we expect), it may still make sense to maintain a downward sloping consumption path (in real dollars) throughout retirement. Barring scenarios that involve cryogenically freezing a body or other attempts to attain life after death, it is simply a mathematical fact that the probability we are alive one year from now is greater than the probability that we are alive two years from now. Thus, there’s a rational case for being present biased even when adequately accounting for longevity risk. Of course, we could just incorporate decreasing spending into a Monte Carlo analysis, but this may provide a consumption path that is too rigid relative to the reality experienced, whereas dynamic programming (presuming the assumptions remain accurate) provides guidance on how consumption should change based on the investment returns experienced.

Another strength of dynamic programming is that it can more adequately address bequest utility (i.e., our desire or willingness to leave over unused principal to the next generation). Given the conservativeness that is inherently built into retirement distribution strategies such as the 4% safe withdrawal rate strategy, retirees blindly adhering to this rule may wind up with significantly more bequest than they desire. One potential limitation of traditional safe withdrawal rate methodologies like this is that they test against historically worst case scenarios. This may be the appropriate benchmark to test against given a retiree’s risk profile (or perhaps not even conservative enough), but this approach potentially ignores valuable insight as a retiree progresses through retirement.

As an example, suppose a retiree has made it ten years into retirement, avoided catastrophic scenarios, and market valuations provide no reason to be particularly concerned. If this individual sticks with a consistent inflation-adjusted 4% distribution from their time of retirement, they are very likely going to leave a substantial estate. Once they survived the period of greatest sequence of return risk, they are likely on a path that could have supported a greater than 4% withdrawal rate. If this individual has high bequest utility (i.e., they want to leave a big inheritance behind for heirs), perhaps no adjustment is needed, and they can simply feel more confident they will leave a larger estate than they might have anticipated entering retirement. However, if this individual has low (or no) bequest utility and simply wants to spend their money to the extent possible in retirement, then a method that doesn’t adjust spending in light of their low bequest utility and experienced investment returns could unnecessarily leave a substantial (and suboptimal) amount of assets unspent. Dynamic programming better illustrates how these adjustments could be made, both upfront and on an ongoing basis.

To illustrate the potential differences between industry rules of thumb for determining withdrawal and asset allocation strategies and dynamic programming recommendations, Irlam & Tomlinson (2014) found that when comparing stochastic dynamic programming (SDP) versus common industry practices, SDP provided a 38% enhancement in initial retirement portfolio income relative to a 60/40 fixed allocation throughout retirement utilizing a 4% withdrawal rate strategy. Interestingly, utilizing SDP to determine both withdrawal rate and asset allocation only provided about 3% higher initial retirement portfolio income when compared to a 90/10 fixed allocation with a 1/life withdrawal rate strategy. However, because spending paths are not consistent between variable spending strategies, initial withdrawal rates don't necessarily tell the full story. Additionally, many advisors might be wary of investing clients as aggressively as the optimal strategy recommended by SDP, but advisors could constrain the model to lower equity exposures, if necessary to accommodate client portfolio risk tolerance.

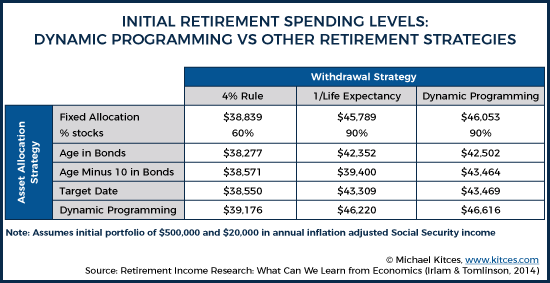
Irlam & Tomlinson (2014) note that one of the reasons for their findings of SDP outperforming rules of thumb, is that many rules of thumb continue to recommend declining equity allocations throughout retirement, even though Samuelson and Merton both found that stable allocations provide higher lifetime utility than declining allocations as far back as 1969. While this highlights another example of the disconnect between the two separate tracks of retirement planning research, interestingly, these same findings have been found in practitioner-oriented research as well. Bengen noted this in his 1996 research and Pfau & Kitces (2014) found similar deficiencies in declining equity glidepaths — yet there hasn’t been much notable change in industry practices. However, Blanchett (2015) did find that a decreasing glidepath resulted in more utility-adjusted overall potential wealth compared to a constant glidepath, so perhaps there is some wisdom embedded within industry practices that hasn’t been fully borne out in prior research, but Blanchett’s study also acknowledged that randomization over a wider number of variables and greater consideration of a specific client’s circumstances and preferences can be beneficial – and dynamic programming provides improvements in both of these areas.

Another strength of SDP models is the potential to take variable distributions during times of poor market conditions. This allows for sustaining higher equity allocations in retirement than may be possible if distributions remain consistent regardless of market conditions. In other words, if retirees are willing and able to adjust their spending to volatile market conditions as a way to manage sequence of return risk, it may be feasible to maintain more volatility in the portfolio itself (which in turn enhances long-term returns and allows for improved retirement spending in the long run as well).

Limitations Of Dynamic Programming

While dynamic programming’s biggest strength is the ability to utilize some elegant models and complex math in order to optimize both asset allocation and distributions, arguably, this could also be one of dynamic programming’s biggest weakness. The insights of dynamic programming are only valuable so long as they reflect reality. If a utility function doesn’t actually capture a retiree’s utility or distributions aren’t actually as flexible as assumed, then the optimization under dynamic programming may not actually be optimizing utility and might even be suggesting actions that would decrease satisfaction in retirement.

And, unfortunately, unlike the inputs into traditional financial plans that tend to be fairly straightforward and easy to comprehend, utility functions and risk aversion coefficients are far more nebulous concepts to most people. It’s hard enough for us to measure abstract concepts like risk tolerance, much less the even-more-complex trade-offs inherent in defining a utility function. Notably, this isn’t an inherent limitation of dynamic programming itself, but it is a limitation of the ability to effectively utilize dynamic programming. In theory, underlying utility functions are only limited by our ability to conceive and develop them, but such an exercise may be a difficult task for most people without a graduate education in economics or mathematics. However, it is also possible that the continued design of new “assessment” tools will allow advisors to better understand how clients feel about various spending and uncertainty trade-offs.

Fortunately, this is one way in which further merging of the currently distinct tracks of practitioner-oriented and economic research can help advisors and researchers collaborate to come up with better solutions. Practitioners can help give insight into what is practical information to act on when working with retirees, while academics can continue to develop better measures of risk tolerance, assessment tools to determine utility, and economic models that more accurately align with retiree archetypes.

Advisors who are interested in utilizing or learning more about dynamic programming can check out Gordon Irlam’s AACalc (free) or Laurence Kotlikoff’s ESPlanner ($950 first year subscription and $750 annual renewal thereafter), which are two retirement planning projection tools that utilize dynamic programming. Both provide some basic utility assumptions that can be used to estimate a retiree’s willingness to engage in trade-offs, with some ability to adjust for their overall aversion to risk and uncertainty.

Like any other planning methodology, dynamic programming has its advantages and disadvantages, though the advantages are significant enough that it will likely play an increasingly large role as planners become more familiar and comfortable with the approach. In particular, the appeal of dynamic programming is the ability to optimize and to illustrate to the client, up front, the benefits of making dynamic adjustments to spending and asset allocation, rather than simply taking a wait-and-see monitoring approach. As a result, dynamic programming can provide a richer and more holistic perspective on how an uncertain future at least might unfold, just as the range of potential outcomes in a Monte Carlo projection provides a richer perspective than just a straight-line projection (and thus why it came into common use).

Ultimately, there’s no one “right” way to do retirement planning. Whether it is Monte Carlo versus historical analysis… goals based versus cash flow based planning... or dynamic programming versus non-optimizing approaches… all will give us different insights which can help guide decision making under risk and uncertainty. But, in the end, if our goal in doing financial planning is at least in part to come up with an actual plan for how to handle an uncertain future, dynamic programming provides some unique functionality that isn't currently available in today’s non-optimizing financial planning software solutions.

So what do you think? Have you used dynamic programming with your clients? Do you think dynamic programming will become more popular in the future? What would make you more likely to adopt dynamic programming with your clients? Please share your thoughts in the comments below!