Executive Summary
With two market "crashes" in the past decade, prospective baby boomer retirees have grown increasingly afraid of the risk that the next market crash could topple their retirement if it comes at the wrong time. This fear has been exacerbated by the recent stream of research on safe withdrawal rates, that highlights how an unfavorable sequence of returns in the early years of retirement can derail a retirement plan. Yet the reality is that failure is dictated not simply by the magnitude of the market decline, but the speed at which it recovers. As a result, while clients are increasingly obsessed about the risk of a sharp decline in the markets (or a so-called "black swan event"), the true danger is actually an extended period of "merely mediocre" results that are uncommon but not rare, not a black swan market crash!
The inspiration for today's blog post comes from some research I am working on for the February issue of The Kitces Report, looking at how we as planners use Monte Carlo analysis to evaluate the risks to a retirement plan and the implications of bad markets. In discussing some of this work with a colleague, I realized how much of a misconception has embedded in the mind of financial planners about what really does, and does not, cause a retirement plan to run out of money.
Understanding Sequence Of Return Risk
For instance, assume the client has a balanced portfolio, with a long-term expected return of 8%, and a standard deviation of 15%. Accordingly, we look at three potential "problem" scenarios:
- In a market crash, the portfolio drops 22% in a single year, and then experiences a sharp recovery and rallies almost 50% the following year (albeit from a lower base) to get back to the original growth rate.
- In an extended bear market, the portfolio declines by 5.4% per year for 5 years. At the end of the decline, the portfolio rallies a whopping 23.3%/year for the next 5 years to get back to the original growth trend.
- In a protracted difficult market environment, the portfolio declines by only 1.5% per year but the declines last 10 years. As the markets eventually hit a valuation bottom, the market rallies forth at 18.4%/year for the next 10 years, finally recovering back to the original growth pace after 20 years.
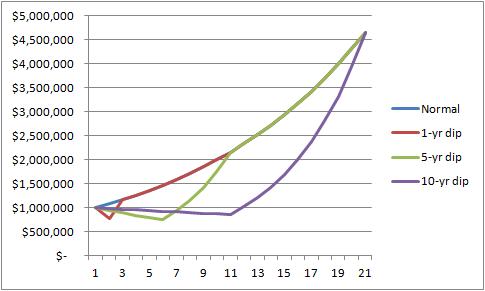 All three of these results represent -2 standard deviation events over a 1-, 5-, and 10-year time horizon, respectively. Thus, these would actually be results that are uncommon but entirely probable in a typical Monte Carlo analysis, although notably clients tend to focus much more on the first scenario (the sharp market decline) than the third scenario (the protracted slightly-declining market).
All three of these results represent -2 standard deviation events over a 1-, 5-, and 10-year time horizon, respectively. Thus, these would actually be results that are uncommon but entirely probable in a typical Monte Carlo analysis, although notably clients tend to focus much more on the first scenario (the sharp market decline) than the third scenario (the protracted slightly-declining market).
If we look at how these portfolios grow over time, we would get the graph to the right, which shows the results of the 1-year, 5-year, and 10-year dips. Ultimately, the recovery rallies get all of the portfolios back on the same track, whether it's a fast decline with a fast recovery or a slower decline with a slower recovery.
But these results simply assume that the client stays invested, with no cash flows in and out of the portfolio. Of course, if the client has no need to take any distributions from the portfolio, there is time to wait. But what happens if these various bear markets strike while the client is taking ongoing withdrawals from the portfolio? How do the results change?
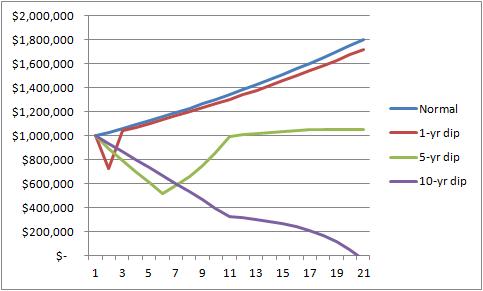 The graph to the right shows the same portfolios modeled above, except this time there is an annual withdrawal at the end of the year of $50,000, which is increased annually assuming 3% inflation. With the client taking ongoing withdrawals, the results are substantially altered. The sharp decline followed by a sharp recovery trails only slightly in the long run, compared to the steady return portfolio. On the other hand, the portfolio that loses 5%/year for 5 years and then recovers ends out dipping far lower, and even after the recovery, finishes with less than 2/3rds the 1-year dip scenario. Conversely, the 10-year dip portfolio - with its tiny decline of only -1.5%/year in returns - is actually the catastrophe, as the portfolio draws down so low with ongoing withdrawals, that by the time the good returns arrive, the portfolio can't recover. It actually runs out of money completely in the final year.
The graph to the right shows the same portfolios modeled above, except this time there is an annual withdrawal at the end of the year of $50,000, which is increased annually assuming 3% inflation. With the client taking ongoing withdrawals, the results are substantially altered. The sharp decline followed by a sharp recovery trails only slightly in the long run, compared to the steady return portfolio. On the other hand, the portfolio that loses 5%/year for 5 years and then recovers ends out dipping far lower, and even after the recovery, finishes with less than 2/3rds the 1-year dip scenario. Conversely, the 10-year dip portfolio - with its tiny decline of only -1.5%/year in returns - is actually the catastrophe, as the portfolio draws down so low with ongoing withdrawals, that by the time the good returns arrive, the portfolio can't recover. It actually runs out of money completely in the final year.
Market Crash Vs A Lost Decade
So what does all of this mean? While we tend to focus on sharp market crashes, sudden declines that recover quickly within just a year or few are not necessarily problematic, whether it's the crash of 1987 (which recovered all of its losses within about a year) or the financial crisis of 2008 (which recovered nearly all of its losses in just over 2 years). Instead of those "black swan" events, that ultimately are just a short-term distraction, what's far more destructive to client portfolios are the extended periods of merely mediocre returns, such as the entire decade from 2000 to 2010, or from 1966 to 1976. And notably, these results are not black swans; the examples here are all simply -2 standard deviation events, such as having a balanced portfolio that loses 1.5%/year and is down 14% after a decade. These are scenarios that Monte Carlo analysis already models; we just don't tend to focus on them very much.
The bottom line is that when we talk about the impact of adverse markets and return sequencing on retired client portfolios, the point is not the risk of short-term volatility. It's the risk of extended periods of time that generate merely mediocre below-average returns. And as history - and even normal distributions - show, these events may be uncommon, but they are not extremely rare, and they're certainly not black swans. They are risks that can be, and should be, planned for.
So what do you think? Which do your retire clients fear more: a 20%+ drop in their balanced portfolio in a single year, or a mere 1.5% decline every year for a decade? Do your clients understand which scenario is worse? Would this impact how you design retired client portfolios?





I think this article is enormously important insofar as it acknowledges the utility of time and time horizon in understanding the complimentary roles of risk management and compounding.
Interestingly, it makes an observation contrary to traditional thought: that time is not always your friend even over the long term. Indeed it is a wasting asset that narrows the opportunities to recover lost returns.
Great work!
Investors need to have alternative spending plans that account for any of these possibilities. (Of course, depending on the actual circumstances, even plans B and C might not be successful. Nobody is promised absolute, locked down financial security. We do the best we can.)
A good approach is to have spending components grouped into needs, wants and wishes and be able to cut out the wants and wishes and still have a fulfilled life. We’ve (many of us) become spoiled in this country during the last half century. A friend of mine just returned from India and his first comment was, “When you include all those people, I’m in the 1%.)
It would be interesting to see how a retiree using decision rules would fare in each scenario.
Michael –
By illustrating so dramatically the adverse effect of a series of below-average years early in retirement, you have put a new spotlight on the question of whether or not Monte Carlo simulations should include some sort of serial correlation.
It’s reported that in U.S. stock market history, over longer time horizons such as 30 years there’s been reversion toward the mean, which is “favorable” –- reducing probabilities of the adversity you illustrate, and generally reducing long-term-results uncertainty. But for much shorter time horizons, momentum has dominated, which would increase likelihood of the adversity you’ve illustrated.
But from what I’ve seen, there are two strong arguments against trying to incorporate these serial correlations in Monte Carlo simulations:
1. That in doing so we would be building in reduction of longer-term uncertainty with pitifully little evidence. In the history since 1926, we have only two non-duplicative 30-year samples, and no assurance that reversion will continue in the future.
2. We have no basis for determining with precision what return-rate mean to use (and revert toward), and in long-term results this uncertainty dominates all others and should be the focus of our concern.
In your recent JFP article on improving results by adjusting allocations according to market valuations, I think (??) your conclusion depends to some extent on historical reversion toward the mean. Does that research, together with your current explorations in Monte Carlo, lead you toward a conclusion as to whether Monte Carlo should include momentum and reversion-toward-mean? –- and if so, how?
Dick Purcell
PS – What’s so neat about Monte Carlo is that it probabilistically combines the early-years uncertainty you have illustrated with other uncertainties – that for your 30 years, your return-rate average will probably be higher or lower than the mean you assumed, and that deviations along the way will make the result lower than if you got your average every year. If you put 10,000 simulation runs on your graphs, you’d have 10,000 probabilistic combinations of all these uncertainties, together representing a probabilistic assessment of the investment’s future.
I hope you keep investigating and posting on Monte Carlo applied in financial planning!
Dick,
Indeed, I think there are both opportunities and challenges to mean reversion and how to model it.
In the simplified sense, I often state that the fundamental basis for mean reversion in returns is economic growth. If the economy is growing – albeit after some period of difficulty – eventually the rising tide lifts all boats, as stocks ultimately reach yields that will induce buyers in any environment.
Thus, to me both the anchor to validity of mean reversion, and its greatest risk, is the engine of economic growth. If that engine breaks down – e.g., Japan since the late 1980s – all bets are off with respect to both mean reversion and the sustainability of income that’s based on an assumption that stocks will be mean reverting. On the other hand, as long as that engine holds solid, I agree that current Monte Carlo analysis probably OVER-estimates the dispersion of long-term results, even while it may UNDER-estimate short- to intermediate-term dispersion from momentum effects.
Respectfully,
– Michael
Dick,
Just to follow up on this – I’d also note that when Pfau did his research last year on the sustainability of safe withdrawal rates across other countries, the common theme (my characterization, not his) is that countries that had an event that “broke” their economic growth engine had materially lower safe withdrawal rates. Countries that merely had “moderate” disasters from which they recovered had withdrawal rates only slightly dissimilar from our own.
– Michael
Michael –
Thanks for the replies.
I think that in FP use of Monte, this is THE dominant question: mean reversion versus “what mean?”
US history shows VERY strong mean reversion. Over in Bogleheads, mathematicians reported it so strong that for simulating 30-year results (not individual years along the way), to approximate dispersion of 30-year-result evidence in U.S. history, you’d use an annual SD of only about half the single-year SD. (Based on historical observations of that kind, I roughed out a curve of “SD shrinkage” versus time horizon for which results are to be assessed, which I’ll try to find and send you.)
There’s also your growth reasoning which supports reversion.
But what mean? Even without reversion, return-rate mean is the dominant unknown input in terms of effect on long-term-result distributions. We don’t have enough history to be sure our calculated mean is not off “true” historical mean by 2% or more. And whatever the “true” mean of the U.S. 20th century was, maybe that of our 21st century will be lower — developing nations = more competition. If we lower the return-rate mean by 2% or more, the distribution of long-term result is very very different. Uncertainty-of-mean argues for more dispersion of long-term possibilities. (Uncertainty about SD suggests the dispersion of long-term results should be even greater.)
If we build in mean reversion, we have to define the mean to which things are reverting, which makes our analyses even more dependent on that unknown mean.
???????
What we do at this point is pure random walk with no mean reversion, with three one-click tools for respectively lowering all means, increasing all SDs, and reducing all correlation differences.
Dick Purcell
Dick,
To the extent that ultimately, returns on stocks are tied to economic growth, I would expect that the return-rate mean is tied to economic growth.
Which is notable because the trend line for economic growth itself is not stable over extended periods of time as countries experience structural change.
– Michael
Hi Michael
I like the article, as with many of your comments it really shows why retirment is different to what we are all used to.
The point about the length of time the market is away from the trend is critical in the drawdown phase. The longer the capital is below trend, the more you are selling your capital at lower prices- something very bad at sustaining the investment.
I’d be interested to see how something like -30% +30% and then a recovery over 10 years to get back to the trend fares. This would show the recovery from a typical market slump from and “overvalued” level rather than ‘fair value’.
Also,Dick, 4.1.1.1, the SD shrinkage that you get is only in the annualised percentage returns. If you look at the actual dispersion of dollars, it keeps increasing over time.
What about a 4% safe withdrawal rate in the initial year? What would the decade long decline look like if initial withdrawals were only $40,000 instead of $50,000?