Executive Summary
For retirees who don’t wish to take any market risk, one of the most straightforward retirement income strategies is to simply purchase a bond ladder that will provide the desired cash flows in each year of retirement. Ideally, the payments are secured out to an advanced age, “just in case” the retiree lives that long… with the obvious caveat that if the retiree doesn’t actually live that long, there will be a lot of money left over that “could have” been spent but wasn’t. But that’s simply the risk of an “unknown” retirement time horizon.
In the case of a (lifetime) annuity, on the other hand, the time horizon is known, at least in the aggregate – because with enough people, the mortality rate actually becomes highly predictable, even if it isn’t known exactly which people will pass away from one year to the next. Yet by knowing that at least some people will die each year, an annuity can pay out a portion of the funds that will have been left behind by those decedents, effectively providing larger guaranteed payments for the group than any one individual could have generated on his/her own.
These “excess” payments are known as “mortality credits”, and represent a unique contribution of (lifetime) annuities that simply doesn’t exist with an individual bond ladder. In fact, the potential for mortality credits means that, for any given maximum potential life span, annuities can actually pay out significantly more than what any individual could enjoy on his/her own, as the contribution of principal and interest and mortality credits will always be greater than the underlying principal and interest alone! Conversely, though, the benefit of mortality credits exists only by virtue of the fact that the other annuitants – and not the annuity owner’s heirs – will benefit from any unused funds that are left over; in fact, trying to protect against an annuity loss in the event of early death, and protect heirs, actually eliminates much of the benefit that annuities are meant to provide in the first place!
Funding Retirement With A Bond Ladder
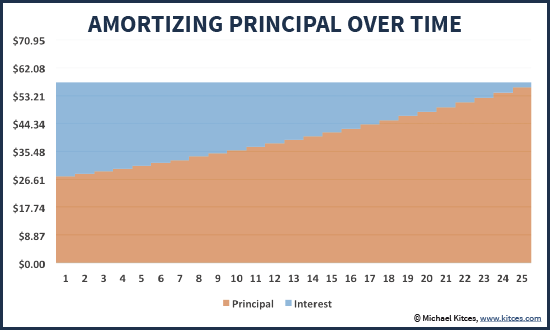
Imagine for a moment that a prospective 70-year-old retiree wishes to secure his remaining 25-year retirement (protecting against the “danger” of living to age 95) without taking any (stock) market risk. Instead, the retiree will simply buy a series of bonds that will provide the maximum possible level payments for the next 25 years (on top of his Social Security payments).
Assuming an average bond return of 3% (given current interest rates), the retiree could effectively amortize principal over a 25-year time horizon by spending $57.43/year for each $1,000 in the portfolio; like a mortgage amortization but in reverse, the early years’ payments will be primarily interest (growth) on the bonds and just a little bit of principal, and by the end almost all of each (outbound) payment will be principal and very little interest as the remaining principal balance approaches zero.
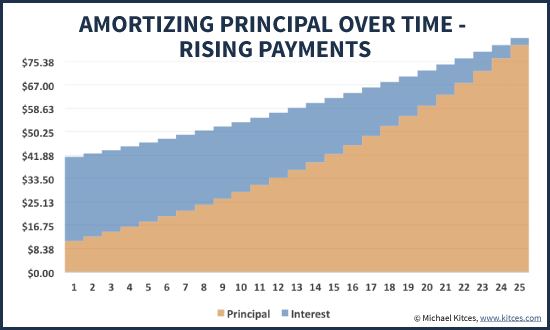
Of course, retirees anticipating inflation may prefer to secure a rising stream of payments rather than level payments – either by funding a bond ladder with TIPS, or simply by structuring the planned withdrawals to rise over time. Such a structure can still be accomplished; it will simply mean the payments start smaller in the early years (and require less in principal liquidations in the early years), and then rise (drawing increasingly heavily on principal) over time.
For instance, the chart below shows the result if the desired payment stream is one that rises by 3% per year to keep up with inflation; the first payment is $41.20, and the last is $83.75, with the early payments funded primarily by interest and the later ones primarily from principal.
Of course, the caveat of this approach is that the retiree doesn’t necessarily know how long he is going to live. And even if the assumption of a 25-year retirement time horizon is “highly conservative” given his health and longevity – such that he doesn’t fear outliving it – there is still the “challenge” that the retiree might live less than 25 years. From the perspective of his heirs, living far less than 25 years may not necessarily be “bad” news – as it simply means there will be a nice inheritance – but it is unfortunate at least in retrospect for the retiree, as it means he could have actually spent more during his lifetime, if only he had known in advance when his time would come.
Pooling Retirement Funds For More Efficient Retirement Spending
At the most basic level, the value of using an (immediate lifetime) annuity to fund retirement income is that it “solves” for the challenge of the unknown time horizon and uncertain mortality (whether living too short or too long), by relying on the law of large numbers to create a predictable time horizon for a large group of retirees in the aggregate.
For instance, imagine there are 25 retirees similar to the one above, each trying to solve for the same problem of spending down a portfolio of fixed assets over a “maximum” time horizon, each taking the “conservative” spending amount necessary to fund the whole time period, even though virtually none of them will actually live that long. Instead of having each retiree fund his/her own portfolio individually, though, the group decides to pool their money together, with the goal of paying each their respective share of principal and interest over time.
As long as the money is invested the same way it would have been, and each participant in the pool of funds requires a payout over their 25-year time horizon, there is no difference in the results; each individual’s share of the payments will be the same as what he/she could have accomplished individually, each protecting against the “danger” of living 25 years.
However, because not everyone will actually live for 25 years, structuring payments in this manner will – as in the case of an individual – likely result in a large account balance left over at the end. In fact, having a large account balance in the end is virtually assured with a group of 25 people, because it’s highly improbable that all of them will live the entire time period. We may not know which people will pass away during the intervening years, but mathematically the odds are overwhelming that at least some of them will.
Furthermore, with enough people (perhaps not 25, but certainly 25,000 or 250,000), it’s actually possible to predict with a high degree of accuracy exactly what percentage of the group will be alive from year to year (a phenomenon known as the “law of large numbers”, where the random variability of mortality on an individual basis “averages out” to consistent results in the aggregate).
The reason this matters is that when it’s known (at least in the aggregate) what proportion of the participants will not live to the maximum 25-year time horizon (or any particular year along the way), it becomes “safe” to begin spending some of that anticipated-to-be-left-over money, in advance, knowing that the number of people requiring distributions from the remaining pool of money will decline over time as participants pass away.
How Mortality Credits Increase Payments To A Pool Of Retirees
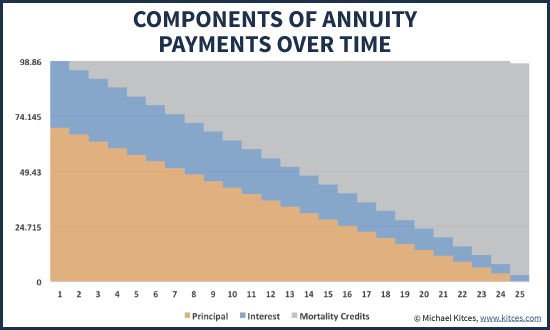
For a simplified example of how this payment structure would work, imagine for a moment that with our group of retirees, our “known” mortality rate is that 1 person on average will pass away each year. We don’t know which person it will be, but simply given the average health of the group, on average one person will die every year. As a result, while there are 25 people around to receive the first payment, only 24 will still be alive to receive the second, 23 will get the third, etc., until there is only 1 (lucky) person expect to be alive by the 25th year to receive the last payment.
Given our earlier assumption of a 3% interest rate, and this new mortality assumption, we can now calculate what the anticipated (level) payment would be every year, that spends down the principal and interest over the 25-year time horizon, but with a decreasing series of payments since fewer distributions must be made as the participants pass away. As it turns out, the payment comes out to be $98.86/year for each $1,000 contribution made by each individual.
Notably, an annual payment of $98.86/year for a $1,000 contribution is significantly higher than the $57.43 that any one individual could have achieved with the same $1,000, the same time horizon, and the same assumed growth rate. The whopping 70% difference in payments occurs because, as noted earlier, each individual has to assume a 25-year time horizon for each person (not knowing who will live and who will not), while the group in the aggregate can reliably assume a shorter time horizon for some of the individual payments (not knowing which people will pass away, but being certain that some will).
In turn, what this actually means is that some people will put in $1,000 and only receive only a few $98.86 payments (in fact, one person is assumed to only receive one payment), while a few will put in the same $1,000 and receive 20+ payments of $98.86/year each. Those who don’t live very long will leave a large balance remaining, which helps to fund the payments for those who actually do live a long time.
The leftover dollars from those who don’t live very long, used to fund the payments to those who do, form what are called “mortality credits”, and represent the additional amount of dollars that can be paid above and beyond principal and interest alone, in anticipation of the mortality of at least some of those participating in the pool. In essence, mortality credits are what make it possible to fund $98.86/year to a group of 25 people for 25 years, even though each person’s funds individually could only cover $57.43/year of payments. On a year-by-year basis, mortality credits make up a larger and larger portion of each payment over time, as more and more people have passed away to fund the fewer and fewer that remain.
Notably, in the real world the mortality rate for retirees is not a flat 4% (1 out of every 25 people) per year; instead, the mortality rate is lower for early retirees, and then climbs higher for older retirees. As a result, in practice a “real world” mortality curve would have a slightly smaller contribution of mortality credits in the early years, a slightly larger contribution in the later years, and the total payments-per-$1,000 would be lower (as more people would survive longer on average). Nonetheless, conceptually the contribution of mortality credits remains the same; it allows for annuities to pay out significantly more to a pool of retirees than the equivalent portfolio could pay to each of those retirees individually.
Annuity Mortality Credits Vs. Legacy Bequests
One of the classic “caveats” to annuitization is the fact that assets, once annuitized, have no remainder value to leave to heirs; while some people will purchase an (immediate) annuity and live a long time (and receive their original principal and then some in return), others will make the purchase and then die unexpectedly, forfeiting what might have been a significant legacy bequest. (Of course, the illiquidity of annuitization can also be concern, especially for those of limited means who might need the funds to handle unexpected health care shocks in retirement.)
Yet the reality is that with annuitization, the decision to give up any legacy bequest (or liquidity along the way) is what makes mortality credits possible in the first place. While theoretically any remaining “unused” funds could be set aside to be repaid at death – and in point of fact, getting an immediate annuity with a “refund guarantee” of unrecovered principal does exactly that – the act of doing so also converts an immediate annuity that pays principal, interest, and mortality credits into one that simply pays principal and interest until principal is recovered (with no accumulation of mortality credits, at least in the early years).
In other words, obtaining an annuity that protects principal in the event of early death eliminates most of the actual benefit of purchasing the annuity in the first place, because “keeping a legacy” and “accumulating mortality credits” are the opposite sides of the same coin; if the remainder is “kept” for heirs, it cannot be used to fund higher payments for the group in the aggregate!
For instance, if the earlier example of an immediate annuity for 25 people included a guarantee that anyone who died early would continue to receive payments until all principal was recovered, then all payments for the first 12 years would be guaranteed for all participants. As a result, only those who died in the last half of the 25-year time period would contribute to mortality credits at all. And by accumulating mortality credits for only half the time period, the payments themselves would be cut significantly, from $98.86/year to only $82.20/year; while this is still an improvement over just amortizing principal and interest for 25 years, it cuts the benefit of mortality credits by nearly 40%!
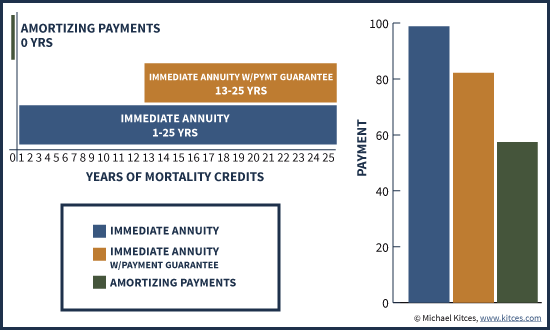
The bottom line, though, is simply this: for a given time horizon, annuities have the potential to produce greater payments than can be achieved from a fixed portfolio alone – even if the annuity company invests the funds in the exact same manner – due to the presence of mortality credits. And while lifetime immediate annuitization also presents the risk of “losing” out on any remaining principal as a legacy in the event of early death, it is the fact that the principal is at risk which makes mortality credits possible in the first place. And by trying to limit the “downside” risk of early death with an annuity, retirees may forfeit a significant portion of the mortality credits they were trying to obtain by using the annuity in the first place!